Альбрехт Дюрер - Трактаты

Но чтобы сделать это понятным юношам для их практической работы, я изображу для них точку прикосновением пера и напишу рядом слово «точка», дабы ее обозначить: точка • Если же теперь протянуть эту точку от ее первоначального места до другого конца, то это называется линией, и эта линия представляет собой длину без всякой толщины и ширины и может быть протянута сколь угодно далеко. Эту линию я нарисую здесь пером в виде прямого штриха и напишу на ней название «линия»: линия, дабы через посредство прямой черты можно было постигнуть разумом невидимую линию, ибо таким путем внутреннее понятие находит выражение во внешнем произведении. Поэтому я намереваюсь рисовать рядом все вещи, которые я буду описывать в этой книжечке, чтобы юноши видели все, что я делаю, изображенным перед глазами и тем лучше бы это поняли. Теперь следует заметить, что линии могут быть проведены различным образом, и особенно [важны] три линии, из которых можно многое сделать. Это, во-первых, прямая линия, во-вторых, линия окружности и затем еще кривая линия, которая делается от руки или может быть проведена от точки к точке, в чем некоторые проявляют искусство, выводя из нее много различий. И я не знаю лучшего наименования для такой кривой линии, нежели извилистая линия [40] В тексте: «Schlangen lini» – буквально «змеевидная линия». Термин этот, употреблявшийся в то время в математике, сохранился и поныне для обозначения извилистой линии. , ибо она может быть проведена туда и сюда, как угодно. И чтобы это было вполне понятно, я нарисовал их здесь внизу.

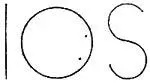
Типы линий

Следует заметить, что имевшиеся выше в виду три линии могут быть проведены длинными или короткими. И если стремиться достигнуть этого, не будучи стесненным временем, то прямая линия может быть продолжена бесконечно вовне или же она может быть представлена наименьшей. Ее можно применять трояким образом: как отвесную, поперечную [41] В тексте: «aufrechte lini» и «zwerch lini». Этими терминами Дюрер пользуется для обозначения вертикальной и горизонтальной линий. В дальнейшем мы везде сохраняем эту терминологию. или косую. Линию же окружности можно употреблять целиком или частями. И она не может быть сделана более длинной, чем от начала и снова до того же места, где она началась; если же провести ее дальше, она опять вернется на прежний путь. Эта линия окружности может быть сделана большой или малой. Если же заставить ее подниматься вверх или опускаться вниз, то из нее получится извилистая линия. Извилистую же линию можно изменять бесконечно – в длину, вдаль, вверх или вниз, – благодаря чему можно сделать много удивительных вещей. И если, как известно, можно сделать много редкостных вещей при помощи одной только линии – о чем ничего не ведают те, кто об этом не размышляет, и здесь тоже об этом будет мало сказано, – нетрудно представить себе, чтó можно сделать с помощью двух, трех или многих линий, и особенно если применять вместе все три типа линий со всеми их разновидностями. Ибо можно сделать много таких линий, которые не могут быть проведены без помощи других. Также следует знать, что такое параллельные линии, называемые так по-латыни, которые я на нашем немецком языке буду называть парными [42] В тексте: «bar linien». Мы сохраняем везде этот термин и вводим слово «параллельные» только в тех случаях, когда им пользуется сам Дюрер. . Это такие линии, которые всегда идут на одном расстоянии друг от друга, будь то прямые, извилистые или линии окружности… [43] Далее следуют определения плоской фигуры и трехмерного тела.

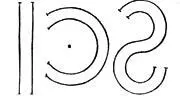
Параллельные линии

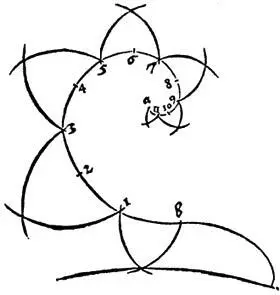
Спиральную линию [44] В тексте: «Schnecken lini» – буквально «улиточная линия». Термин этот сохранился и в настоящее время для обозначения спирали. я вычерчиваю так: я провожу отвесную линию, которую обозначаю вверху а и внизу b , и делю ее тремя точками с, d, e на четыре равные части. Затем я делю часть de точечкой f на две равные части. Затем я ставлю слева от линии букву g , справа h . Затем я беру циркуль и ставлю его одной ножкой в точку d , а другой в точку а и провожу линию на стороне h до точки b внизу. Затем я беру циркуль и ставлю его одной ножкой в точку f , а другой в точку с и провожу на стороне g линию вниз до точки b . Снова я беру циркуль и ставлю его одной ножкой в точку d и провожу на стороне h другой ножкой линию из точки с до точки е . Затем я ставлю циркуль одной ножкой в точку f , а другой в точку d и провожу на стороне g линию до точки е . Затем я ставлю циркуль на линию аb одной ножкой посередине df , а другой в точку d и провожу оттуда на стороне h линию до точки f . Итак, линия готова и употребляется для многих вещей, и среди прочего – для волюты капители. И чтобы это было более понятно, я провел здесь две поперечные линии из точек а и с от спиральной линии назад… [45] Далее следует описание других способов вычерчивания спирали и применения ее для рисования навершия епископского посоха и побега с листвой, а также описание других видов кривых, прежде всего нескольких типов винтовых линий.

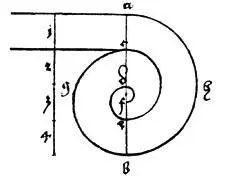
Построение спирали

Эта линия употребляется для епископского посоха.

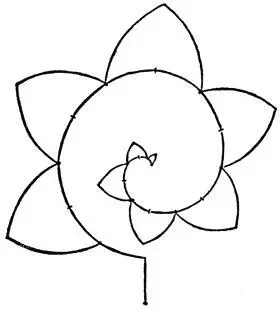
Эта линия употребляется для побега с листвой.

Древние показали, что можно сделать три рода сечений конуса, которые отличались бы друг от друга и не имели бы одинаковой с его основанием циркульной формы. Еще можно сделать сечение посередине конуса, которое будет иметь подобную конусу форму; его не принимают в расчет. Но я хочу научить построению первых трех сечений, каждое из которых дает особую линию, а также вычерчиванию этих линий. Первое сечение ученые называют эллипсом, оно разрезает конус наклонно, не срезая ничего от основания. Этот наклонный срез должен быть сделан с одной стороны выше, а с другой – ниже, так что с одной стороны он ближе к основанию, а с другой – дальше. Второе сечение образует в чертеже линию, парную стороне конуса ab или противоположной, по желанию; его ученые называют параболой. Третье сечение образует в чертеже отвесную линию, парную линии, проведенной из центра конуса вверх до его вершины; это они называют гиперболой. Я не умею назвать эти три линии по-немецки, но мы дадим им наименования, чтобы можно было их узнавать. Эллипс я буду называть яйцевидной линией, потому что он почти подобен яйцу. Парабола пусть называется зажигательной линией, ибо если сделать из нее зеркало, то оно будет зажигать. Гиперболу же я буду называть вилообразной линией.