Андрей Павлов - Геометрия: Планиметрия в тезисах и решениях. 9 класс

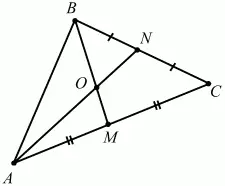
Рис. 110.

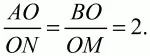
Для четырёхугольников:

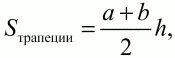
где а, b – длины оснований;

h – высота трапеции.

Площадь параллелограмма со сторонами а, b и углом ? между ними вычисляется по формуле S = ab sin ?. Можно также воспользоваться формулой:

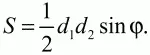
где d1, d2– длины диагоналей, ? – угол между ними (или S = aha, где ha – высота).

Для произвольного выпуклого четырёхугольника (рис. 111):

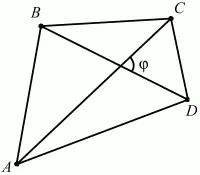
Рис. 111.

Для правильного n-угольника:

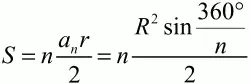
(R и r – радиусы описанной и вписанной окружностей, аn – длина стороны правильного n-угольника).

Для окружности и круга (рис. 112):

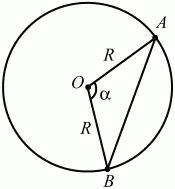
Рис. 112.

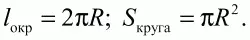
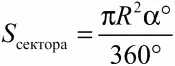
и 1\2R2?, если ? выражен в радианах.

Sсегмента = Sсектора – Sтреугольника.

Если даны точки A(x1; y1) и В(х2; у2), то

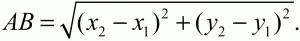
Уравнение прямой АВ:

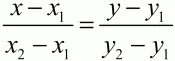
легко приводится к виду ах + by + с = 0, где вектор n = (а, b) перпендикулярен прямой.

Расстояние от точки А(х1; у1) до прямой ах + by + с = 0 равно

Расстояние между параллельными прямыми ах + by + с1 = 0 и ах + by + с2 = 0 равно

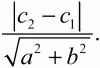
Угол между прямыми а1х + BLу + с1 = 0 и а2х + b2y + с2 = 0 вычисляется по формуле:

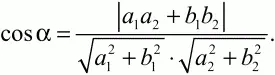
Уравнение окружности с центром в точке O(x0, y0) и радиусом R:(x – xo)2+ (y – yo)2= R2.

1. а) Какое вы знаете свойство вертикальных углов? (1)

б) Докажите это свойство. (1)

2. а) Сформулируйте признак равенства треугольников по двум сторонам и углу между ними. (1)

б) Докажите данный признак. (1)

3. а) Сформулируйте признак равенства треугольников по стороне и двум углам. (1)

б) Докажите данный признак. (1)

4. а) Перечислите основные свойства равнобедренного треугольника. (1)

б) Докажите эти свойства. (1)

в) Докажите признак равнобедренного треугольника. (1)

5. а) Сформулируйте признак равенства треугольников по трём сторонам. (1)

б) Докажите данный признак. (1)

6. Докажите, что две прямые, параллельные третьей, параллельны. (2)

7. а) Сформулируйте признаки параллельности прямых. (1)

б) Докажите эти признаки. (1)

в) Докажите обратные теоремы. (1)

8. Докажите теорему о сумме углов треугольника. (1)

9. Докажите, что внешний угол треугольника равен сумме двух внутренних, не смежных с ним. (1)

10. а) Сформулируйте признаки равенства прямоугольных треугольников. (1)

б) Докажите признаки равенства прямоугольных треугольников по гипотенузе и катету; по гипотенузе и острому углу. (1)

11. а) Докажите, что из точки, не лежащей на данной прямой, можно опустить на эту прямую единственный перпендикуляр. (1)

б) Докажите, что через точку, лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной. (1)

12. а) Где лежит центр описанной около треугольника окружности? (1)

б) Докажите соответствующую теорему. (1)

13. а) Где лежит центр вписанной в треугольник окружности? (1)

б) Докажите соответствующую теорему. (1)

14. Докажите свойство касательной к окружности. (1)

15. а) Какие вы знаете свойства параллелограмма? (1)

б) Докажите эти свойства. (1)

16. а) Какие вы знаете признаки параллелограмма? (1)

б) Докажите эти признаки. (1)

17. а) Какие вы знаете свойства и признаки прямоугольника? (1)

б) Докажите эти свойства и признаки. (1)

18. а) Какие вы знаете свойства и признаки ромба? (1)

б) Докажите эти свойства и признаки. (1)

19. а) Какие вы знаете свойства и признаки квадрата? (1)

б) Докажите эти свойства и признаки. (1)

20. а) Сформулируйте теорему Фалеса. (1)

б) Докажите эту теорему. (1)

21. а) Сформулируйте обобщенную теорему Фалеса (теорему о пропорциональных отрезках). (1)

б) Докажите эту теорему. (2)

22. а) Какие свойства средней линии треугольника вы знаете? (1)

б) Докажите эти свойства. (1)

23. а) Какие вы знаете свойства средней линии трапеции? (1)

б) Докажите эти свойства. (1)

24. а) Сформулируйте теорему Пифагора. (1)

б) Докажите теорему Пифагора. (1)

в) Сформулируйте и докажите обратную теорему. (2)

25. Докажите, что любая наклонная больше перпендикуляра, и что из двух наклонных больше та, у которой больше проекция. (1)

26. а) Сформулируйте неравенство треугольника. (1)

б) Докажите неравенство треугольника. (2)

27. Даны координаты точек A(х1; у1) и В(х2; у2).

а) По какой формуле вычисляется длина отрезка AB? (1)

б) Выведите эту формулу. (1)

28. Выведите уравнение окружности с центром в точке А(х0; у0) и радиусом R. (1)

29. Докажите, что любая прямая в декартовых координатах х, у имеет уравнение вида ах + by + с = 0. (2)

30. Напишите уравнение прямой, проходящей через точки А(х1; у1) и В(х2; у2). Ответ: обоснуйте. (2)

31. Докажите, что в уравнении прямой у = kx + b число k есть тангенс угла наклона прямой к положительному направлению оси абсцисс. (2)

32. а) Какие вы знаете основные свойства движений? (2)

б) Докажите эти свойства. (3)

33. Докажите, что:

а) преобразование симметрии относительно точки является движением; (3)

б) преобразование симметрии относительно прямой является движением; (3)

в) параллельный перенос есть движение. (3)

34. Докажите теорему о существовании и единственности параллельного переноса. (3)

35. Докажите, что абсолютная величина вектора kа равна |к| ? |а|, при этом направление вектора kа при а ? О совпадает с направлением вектора а, если k > 0, и противоположно направлению вектора а, если к < 0. (1)