Андрей Павлов - Геометрия: Планиметрия в тезисах и решениях. 9 класс

Но тут же ученику предложили доказать, что сумма углов в треугольнике равна 180°. Учащийся сослался на свойства параллельных прямых. Но сами свойства параллельных прямых он стал доказывать на основе признаков параллельности прямых. Круг замкнулся. Поэтому в повторении теории будьте последовательны и внимательны. При чтении доказательства теоремы особое внимание обращайте на то, где в доказательстве использованы условия теоремы, какие ранее доказанные теоремы при этом использовались.

В настоящем параграфе формулировки теорем приведены по учебнику А. В. Погорелова «Геометрия. 7–9 классы».

Свойства параллельных прямых.

Две прямые, параллельные третьей, параллельны (рис. 57).

(а||с, b||с) ? а||b.

Рис. 57.

Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180° (рис. 58).

а||b ? ? = ?

? + ? = 180°.

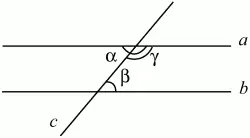
Рис. 58.

Признаки параллельности прямых.

Если при пересечении двух прямых третьей образующиеся внутренние накрест лежащие углы равны, то прямые параллельны (рис. 59):

внутренние накрест лежащие углы равны ? а||b.

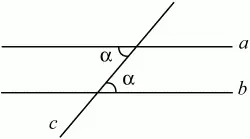
Рис. 59.

Если при пересечении двух прямых третьей сумма образовавшихся внутренних односторонних углов равна 180°, то прямые параллельны (рис. 60):

а||b.

Рис. 60.

Если при пересечении двух прямых третьей образующиеся соответственные углы равны, то прямые параллельны (рис. 61):

а||b.

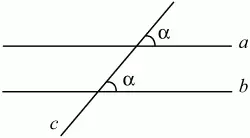
Рис. 61.

Теоремы о существовании и единственности перпендикуляра к прямой. Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну (рис. 62).

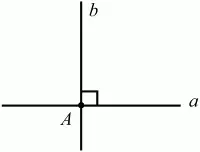
Рис. 62.

Прямая b – единственная прямая, проходящая через точку А перпендикулярно а.

Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один (рис. 63).

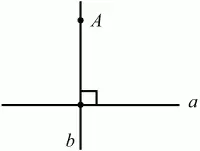
Рис. 63.

Прямая b – единственная прямая, проходящая через точку А перпендикулярно а.

Связь между параллельностью и перпендикулярностью.

Две прямые, перпендикулярные третьей, параллельны (рис. 64).

(а ? с, b ? с) ? а||b.

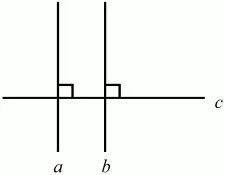
Рис. 64.

Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой (рис. 65):

(а ? b, b||с) ? а ? с.

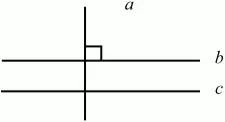
Рис. 65.

Свойство вертикальных углов.

Вертикальные углы равны (рис. 66):

? = ?.

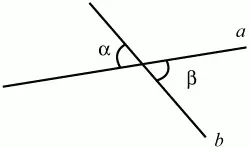
Рис. 66.

Свойство углов равнобедренного треугольника. В равнобедренном треугольнике углы при основании равны. Верна и обратная теорема: если в треугольнике два угла равны, то он равнобедренный (рис. 67):

АВ = ВС ? ?А = ?С.

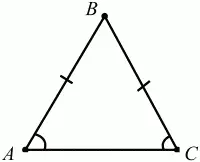
Рис. 67.

Теорема о сумме углов в треугольнике.

Сумма внутренних углов треугольника равна 180° (рис. 68):

? + ? + ? = 180°.

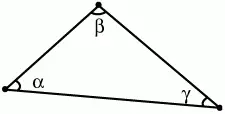
Рис. 68.

Теорема о сумме углов в выпуклом n-угольнике.

Сумма углов выпуклого n-угольника равна 180°?(n – 2) (рис. 69).

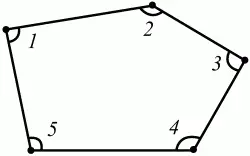
Рис. 69.

Пример:?1 + ?2 + ?3 + ?4 + ?5 = 180°?(5–2) = 540°.

Теорема о внешнем угле треугольника.

Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним (рис. 70):

? = ? + ?.

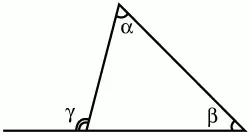
Рис. 70.

Теорема о величине вписанного в окружность угла.

Угол, вписанный в окружность, равен половине соответствующего q центрального угла (рис. 71):

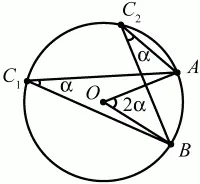
Рис. 71.

Признаки равенства треугольников. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис. 72).

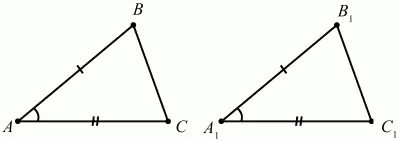
Рис. 72.

?ABC = ?A1B1C1 т. к. АB = А1В1, АС = А1С1 и ?A = ?A1.

Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 73).

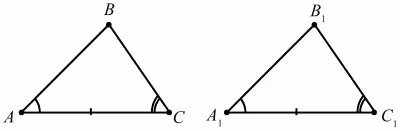
Рис. 73.

?ABC = ?A1B1C1 т. к. АC = А1C1, ?A = ?A1, ?C = ?C1.

Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны (рис. 74).

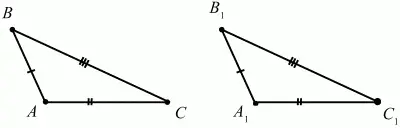
Рис. 74.

?ABC = ?A1B1C1 т. к. АB = А1B1, АC = А1C1, BC = B1C1.

Признаки равенства прямоугольных треугольников.

Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны (рис. 75).

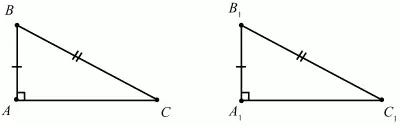
Рис. 75.

?ABC = ?A1B1C1 т. к. ?А = ?А1 = 90°; BC = B1C1; AB = A1B1.

Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие треугольники равны (рис. 76).