Андрей Павлов - Геометрия: Планиметрия в тезисах и решениях. 9 класс

4. В равнобедренной трапеции ABCD угол А = 30°, угол ACD = 135°, AD = 20 см, ВС = 10 см:

а) докажите, что АС – биссектриса угла ВАС;

б) найдите периметр трапеции.

5. В треугольнике ABC АВ = 17 см, ВС = 25 см. Высота BD равна 15 см. Найдите площадь треугольника.

1. Свойства ромба, прямоугольника, квадрата (с доказательством).

2. Уравнение прямой (без вывода). Смысл коэффициента k в уравнении у = kx + b (без обоснования).

3. Периметр треугольника равен 35 см. Найдите отрезки, на которые биссектриса треугольника делит противоположную сторону, если две другие стороны треугольника равны 12 и 16 см.

4. Найдите радиус окружности, вписанной в треугольник со сторонами 20, 20 и 24 см.

5. Как изменится длина окружности, если площадь соответствующего ей круга уменьшится в 441 раз?

1. Теорема Фалеса (с доказательством).

2. Вектор. Действия над векторами. Базис на плоскости. Теорема о разложении вектора по базису (без доказательства).

3. Дана трапеция ABCD. Постройте фигуру, на которую отображается данная трапеция при центральной симметрии с центром А.

4. В треугольнике ABC CD – медиана. Найдите площадь треугольника BDC, если АС = 10 см, ВС = 20 см и угол АСВ = 135°.

5. На рисунке изображена окружность с центром О, АВ = DE. Докажите, что угол АОЕ равен углу BOD (рис. 216).

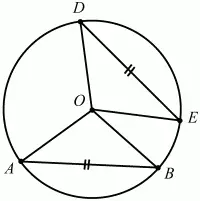
Рис. 216.

1. Свойство средней линии треугольника и трапеции (с доказательством).

2. Длина окружности и площадь круга (без вывода).

3. На рис. 217 угол 1 = 67°, угол 2 = 127°, угол 4 = 67°. Найдите угол 3 (рис. 217).

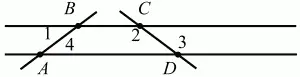
Рис. 217.

4. Диагонали параллелограмма ABCD пересекаются в точке О. Найдите х, у, z, если:

а) АС = х ? АО; б) ВО = у ? DB; в) АВ = z ? CD.

5. В треугольнике ABC АВ = ВС, BD – высота. Через середину высоты проведена прямая, пересекающая стороны АВ и ВС в точках Е и F соответственно. Найдите EF, если BD = h, угол ABC = ?, угол BEF = ?.

1. Теорема Пифагора (с доказательством).

2. Пропорциональность отрезков хорд и секущих окружности (без вывода).

3. Найдите синус, косинус и тангенс острых углов А и В прямоугольного треугольника ABC, если АВ = 13 см, ВС = 12 см.

4. В прямоугольнике ABCD сторона AD равна 10 см. Расстояние от точки пересечения диагоналей до этой стороны равно 3 см. Найдите площадь прямоугольника.

5. В равнобедренном треугольнике ABC с основанием АС серединный перпендикуляр стороны АВ пересекает сторону ВС в точке Р. Найдите угол РАС, если угол ВСА = 65°.

1. Координаты на плоскости. Расстояние между точками (с выводом).

2. Признаки подобия треугольников (без доказательств).

3. Параллельны ли прямые a и b, изображенные на рисунке (рис. 218).

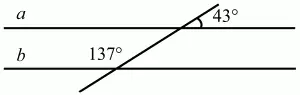
Рис. 218.

4. В прямоугольном треугольнике с углом 30° и меньшим катетом – 6 см проведены средние линии. Найдите периметр треугольника, образованного средними линиями.

5. АВ и АС – касательные к окружности с центром О (С и В – точки касания). Найдите градусную меру меньшей из дуг ВС, если расстояние от центра окружности до точки А равно 8 см, а до хорды ВС – 6 см.

1. Уравнение фигуры. Уравнение окружности (с выводом).

2. Формула для радиуса вписанной в треугольник окружности (без вывода).

3. Найдите площадь равностороннего треугольника со стороной а = 2.

4. В параллелограмме две стороны равны 2 и 3 см, а один из углов 120°. Найдите длину меньшей диагонали параллелограмма.

5. Стороны треугольника равны 4 и 5, а угол между ними 60°. Найдите высоту h, опущенную на третью сторону треугольника.

1. Скалярное произведение векторов. Угол между векторами (с выводом).

2. Формулы для радиуса описанной около треугольника окружности (без вывода).

3. В остроугольном треугольнике ABC высоты АА1 и ВВ1 пересекаются в точке О. Найдите угол ОСА, если угол BAС = 58°.

4. Длина стороны многоугольника равна 3 м, а длина сходственной стороны подобного ему многоугольника равна 48 дм. Найдите периметры этих многоугольников, если их разность составляет 9 м.

5. На рис. 219 ABCD – прямоугольник, AM = BN = СК = DP. Докажите, что MNKP – параллелограмм.

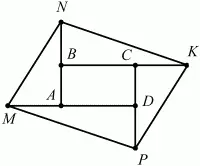
Рис. 219.

1. Теорема о величине вписанного в окружность угла (с доказательством).

2. Аксиомы, теоремы, определения. Пример аксиом.

3. В треугольнике ABC проведена биссектриса AK. Найдите угол В, если угол С = 33°, угол АКС = 110°.

4. В треугольнике две стороны равны 10 и 12 см, а угол между ними 45°. Найдите площадь треугольника.

5. Точка М лежит на диагонали АС параллелограмма ABCD, а точка Н – на его стороне AD, причем AM: МС = 2:1, АН = HD. Выразите вектор MN через векторы а и р где вектор а равен вектору АВ и вектор p равен вектору AD.

1. Теорема косинусов (с выводом).

2. Виды движений на плоскости.

3. Стороны параллелограмма равны 8 и 10 см, угол между ними 60°. Найдите площадь параллелограмма.

4. Длина одного отрезка на 1 см больше второго и на 4 см больше третьего. Могут ли эти отрезки быть сторонами треугольника, периметр которого равен 10 см?

5. Каждая из боковых сторон и меньшее основание трапеции равны 5 см, а один из его углов равен 60°. Найдите радиус окружности, описанной около нее.

1. Теорема синусов (с выводом).

2. Признаки параллельных прямых (без доказательства).

3. Подобны ли два треугольника ABC и А1В1С1, если АС = 14 см, А1В1 = 22 см, В1С1 = 26 см, А1C1 = 28 см, АВ = 11 см, ВС = 13 см.

4. Сторона описанного правильного четырёхугольника на ?3 больше стороны правильного треугольника, вписанного в ту же окружность. Найдите сторону четырёхугольника.

5. Окружность с центром О касается сторон МК, КТ и ТМ треугольника МКТ в точках А, В и С соответственно. Найдите углы треугольника ABC, если угол МКТ = 42°, угол КМТ = 82°.

1. Многоугольники. Правильные многоугольники. Основные формулы для правильных n-угольников (с выводом).

2. Формула Герона (без вывода).

3. Через вершину А треугольника ABC с прямым углом С проведена прямая AD, параллельная стороне ВС. Найдите угол В треугольника, если угол DAB = 43°.

4. В треугольнике АВС АВ = 15 м, АС = 20 м, ВС = 32 м. На стороне АВ отложен отрезок AD = 9 м, а на стороне АС – отрезок АЕ = 12 м. Найдите DE.

5. Каким должен быть радиус окружности, чтобы ее длина была равна разности длин двух окружностей с радиусами 37 и 15 см?