Сергей Коч - … всё во Всём

Однако хозяин, кажется, немного смутился из-за своей последней фразы. Он поспешил перевести разговор на другую тему.

– Признаться, я думал, вы расскажете мне, какие вы видели любопытные артефакты. Вы же, наверное, должны интересоваться материальными свидетельствами старины. Посуда, утварь… Книги…

Я посмотрел на него внимательно, вспомнив свое недавнее «общение» с книгой. Нет, он не мог знать. Невозможно. Моментально мне вспомнились последние видения. Я медленно проговорил:

– Боюсь, что археологи не так уж и много работают с книгами. Книга – слишком хрупкий предмет. Книги читают… переписывают. Книги одних народов читают и переписывают мудрецы из других народов. Аль Хорезми читал и переписывал книги индийских ученых. А потом его книги прочитал великий математик Леонардо Фибоначчи. А про книги индийских ученых почти ничего не известно…

– Ну, что-то всё же известно, – улыбнулся мой собеседник.

– Вы сможете мне о них рассказать?

– А вам это действительно интересно?

– Да.

– Тогда смотрите.

Этот явно не нищий человек, оказавшийся теперь таким простым в общении, и по совместительству – бывший московский студент, вопреки всем правилам поведения с гостями, сидел со мной за столом. Он достал из кармана дорогой Молескин-блокнот и карандаш. Тщательно отогнул страницу с пометками – там были номера и какие-то короткие записи, видимо жалобы или напоминания для посетителей, с таким видом, будто эти записи были недостойны того, что он намеревался изобразить, и нарисовал десятью или одиннадцатью штрихами на белом листке схему.

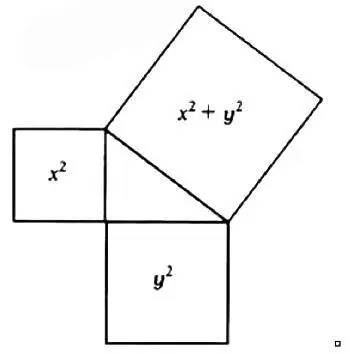
– Как ты думаешь, что это?

Прежде всего я подумал, как хорошо, что он перешел на «ты». Потом подумал по существу вопроса и сказал:

– Это похоже на теорему Пифагора.

– А как ты думаешь, кто нарисовал эту схему?

– Ну, не знаю. А кто?

– Катьяяна. И было это во втором веке до новой эры. А еще этот великий муж был грамматиком, совершенствовал санскрит, вслед за другим великим грамматиком Панини. А еще ребенком он отличался такой памятью и способностями, что мог наизусть повторить целую драму, виденную им в театре.

Вот как звучит выведенный им закон: «Веревка, натянутая вдоль диагонали, и по длине равная диагонали прямоугольника образует фигуру той же площади, что и образованная горизонтальной и вертикальной сторонами».

– Это написано в какой-то вашей древней книге?

– Это «Шульба-сутра», раздел «Веданг». Считается, что эти тексты написаны в 800–600 годах до нашей эры. Хотя, кто знает? Может быть, это первый в мире строительный стандарт.

– Строительный?

– Ну, да. В сущности, это книга, описывающая строительство алтарей. Боги почему-то никогда не строили алтари. Это делали за них люди, – и он опять радостно рассмеялся. – Такие, как я. Я же строитель.

В «Шульба-сутре [9] Шульба-сутра – значительное место занимает преобразование прямоугольника в квадрат, которое равносильно решению квадратного уравнения х2=ав. Проводится сравнение этого преобразования, сделанного авторами редакций «Шульба-сутр» и Евклидом в «Началах», и показывается, что и там, и здесь данное преобразование производится в два этапа, при этом на первом – проделываются идентичные действия. Приводятся и другие аналогии между индийской и греческой математикой (правило, которое в современных терминах имеет вид (а+х)2 = а2+2ах+х2; сходство задач, решаемых в древней Индии и античной Греции; инструменты, которыми пользовались при построении: циркуль и линейка, роль которых в древней Индии играла веревка, закрепленная с одного конца, либо с отмеченными узлами в двух местах; теорема Пифагора и др.). На основе перечисленных аналогий делается вывод, что такое количество совпадений не может быть случайным. » описаны формулы, например, чтобы преобразовать одну фигуру в другую. И ваша теорема Пифагора там есть. Сначала она звучала проще: Веревка (шульба), натянутая по диагонали квадрата, образует фигуру вдвое большей площади, чем исходный квадрат. В таком виде ее написал Бодхайяна. Но про этого мудреца я совсем ничего не знаю – кроме того знания, которое он оставил потомкам.

В те незапамятные времена люди чувствовали красоту арифметики и геометрии. С самого начала им стало понятно, что все фигуры делятся на криволинейные и прямолинейные, а прямоугольные треугольники быстро заняли привилегированное место среди прочих фигур. Два прямоугольных треугольника можно получить, если разделить прямоугольник пополам его диагональю. Привилегированное место в арифметике заняли натуральные числа, которые использовались при счете. В какой-то момент стало понятно, что можно строить прямоугольные треугольники, длины всех сторон которых выражены целыми числами. Открытие равенства суммы квадратов катетов и квадрата гипотенузы было особенным.

Я с необыкновенным вниманием слушал его рассказ, совпадения в истории развития математики разных стран стали «ложиться» друг на друга, дополняя ранее услышанное мной. Мне почему-то вздумалось слегка «подколоть» моего собеседника, я вспомнил все свои скромные познания о науках в Индии и спросил:

– Так ведь Веды – Апаурушея. То есть несотворённые человеком, вечные богооткровенные писания.

Он весело улыбнулся.

– Так боги и книг не писали. А откровения даны через святых мудрецов. А мудрецы-математики, которые проникли в тайну фигуры и числа, разве они недостойны святости?

– Аты как думаешь, они… допустим, слышали какой-то голос? Или просто додумались?

– Просто додуматься совсем не просто. Что это значит – додуматься? Только что ты не знал, а теперь знаешь? А что помогло тебе совершить этот переход? А, может, кто?

Он поставил меня снова в тупик своими вопросами. Я снова стал искать признаки того, что он действительно знает всё, что мне пришлось пережить за последнее время. Ничего на это не указывало. Да и его я точно видел впервые в жизни. Я решился на вопрос:

– Что же получается? Мы постоянно переживаем откровения, и сами не замечаем этого?

– Ты так сказал, – ответил мой собеседник неожиданно строгим голосом. – Но ведь и не все же. Сколько было за всю историю ученых, поэтов, философов? А сколько людей? Откровение не всякому дается.

– Нужно быть избранным, значит?

– Ты так сказал.

Мне захотелось срочно перевести разговор на другую тему, и я спросил:

– А кто придумал цифры? Те, которыми мы теперь пользуемся.

– Кто знает? – подмигнул мне мой собеседник. – Цифры пришли к нам из санскрита, а санскрит, как ты, конечно, знаешь, божественный язык.

Мой неожиданный гуру продолжал: