Стивен Прата - Язык программирования C. Лекции и упражнения (6-е изд.) 2015

Предположим, что в списке необходимо найти конкретный элемент. Один из возможных алгоритмов предусматривает старт поиска с начала списка и последовательный просмотр его элементов; это называется последовательным поиском. Если элементы не упорядочены каким-либо образом, то последовательный поиск — это практически все, что можно предпринять. Если искомый элемент в списке отсутствует, придется просмотреть все элементы, прежде чем можно будет утверждать об этом. (Здесь может помочь параллельное программирование, т.к. разные процессоры могут выполнять поиск в разных частях списка одновременно.)

Последовательный поиск можно улучшить, предварительно отсортировав список. Эго позволяет прервать поиск, если искомый элемент не найден по достижении элемента, который должен был бы следовать за искомым. Например, предположим, что мы выполняем поиск элемента Susan в списке, упорядоченном по алфавиту, и через некоторое время наталкиваемся на элемент Sylvia, так и не найдя элемента Susan. В этом месте поиск можно прервать, поскольку элемент Susan, если бы присутствовал в списке, то он предшествовал бы элементу Sylvia В среднем этот метод может вдвое сократить время поиска элементов, отсутствующих в списке.

В случае упорядоченного списка для поиска можно использовать намного более эффективный метод двоичного поиска.. Вот как он работает. Для начала назовем искомый элемент списка целевым и предположим, что список упорядочен по алфавиту. Затем выберем элемент, расположенный посередине списка, и сравним его с целевым элементом. Если эти два элемента равны, поиск завершен. Если элемент списка в алфавитном порядке предшествует целевому элементу, то целевой элемент, если он

Расширенное представление данных 763

присутствует в списке, должен находиться во второй половине. Если элемент списка следует за целевым, то целевой элемент должен располагаться в первой половине. В любом случае правила поиска уменьшают количество просматриваемых элементов вдвое. Затем этот метод применяется снова. То есть мы выбираем элемент, расположенный посередине остающейся половины списка. Как и ранее, метод либо находит элемент, либо вдвое уменьшает размер просматриваемого списка. Эти действия продолжаются до тех пор, пока элемент не будет найден или пока не будет исключен весь список (рис. 17.11). Описанный метод весьма эффективен. Для примера предположим, что список содержит 127 элементов. При использовании последовательного поиска обнаружение элемента либо установление его отсутствия в списке требовало бы в среднем 64 операции сравнения. В то же время двоичный поиск требовал бы выполнения не более 7 сравнений. Первая операция сравнения уменьшает количество возможных совпадений до 63, вторая — до 31 и т.д., пока шестое сравнение не уменьшит число возможных элементов до 1. После этого седьмая операция сравнения определяет, является ли остающийся элемент целевым.

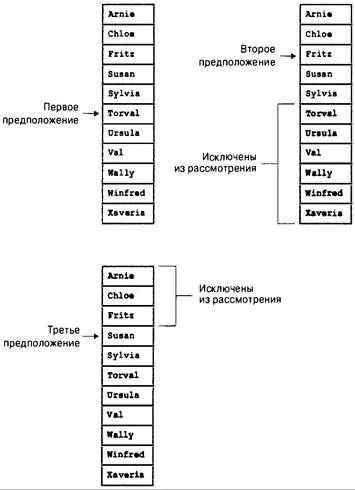
Рис. 17.11. Двоичный поигж элемента Susan

764 глава 17

В общем случае n сравнений позволяют обработать массив, содержащий 2"-1 элементов, поэтому преимущество применения двоичного поиска по сравнению с последовательным поиском становится все более явным по мере увеличения длины списка.

Реализовать двоичный поиск в массиве довольно просто, т.к. для определения средней точки в любом списке или его части можно использовать индекс массива. Для этого нужно сложить индексы начального и конечного элементов части списка и разделить результат на 2.

Например, в списке, состоящем из 100 элементов, первый индекс равен 0, а последний — 99, и начальным предположением является (0 + 99)/2, или 49 (целочисленное деление). Если элемент с индексом 49 располагается слишком далеко по алфавиту, искомый элемент должен находиться в диапазоне 0-48, поэтому вторым предположением становится индекс (0 + 48)/2, или 24. Если 24-й элемент в алфавитном порядке расположен слишком близко, то следующим предположением будет индекс (25 + 48)/2, или 36. Именно здесь в игру вступает возможность произвольного доступа к элементам массива. Она позволяет переходить от одного элемента к другому, не посещая все расположенные между ними элементы. Связные списки, которые поддерживают только последовательный доступ, не предоставляют средства для перехода к точке в середине списка, поэтому прием двоичного поиска нельзя применять к связным спискам.

Как видите, выбор типа данных зависит от решаемой задачи. Если ситуация требует использования списка, размер которого постоянно изменяется за счет частых вставок и удалений элементов, но поиск в котором производится не особенно часто, то лучше выбрать связный список. В тех же ситуациях, когда необходим стабильный список с редкими вставками и удалениями, но частым поиском, лучше применять массив.

А что, если требуется форма данных, поддерживающая как частые вставки и удаления, так и частый поиск? Ни связный список, ни массив далеко не идеальны для таких целей. Наиболее подходящей может оказаться другая форма данных — двоичное дерево поиска.

Двоичные деревья поиска

Двоичное дерево поиска — это связная структура, которая включает в себя поддержку стратегии двоичного поиска. Каждый узел дерева содержит элемент и два указателя на другие узлы, называемые дочерними узлами. Связь между узлами в двоичном дереве поиска показана на рис. 17.12. Основная идея этой структуры состоит в том, что каждый узел имеет два дочерних узла — левый и правый. Порядок элементов определяется тем, что элемент в левом узле предшествует элементу в родительском узле, а элемент в правом узле следует за элементом родительского узла. Э го отношение сохраняется для всех узлов среди дочерних узлов. Более того, все элементы, чья родословная может быть прослежена до левого узла родительского узла, содержат элементы, которые предшествуют родительскому элементу, а все элементы, являющиеся потомками правого узла, содержат элементы, следующие за родительским элементом. Слова в дереве на рис. 17.12 хранятся именно таким образом. Верхняя часть дерева, в отличие от ботаники, называется корнем. Дерево представляет собой иерархическую организацию данных, т.е. данные организованы по рангам, или уровням, причем в общем случае каждому рангу соответствуют ранги, расположенные над и под ним. Если двоичное дерево поиска полностью заполнено, каждый уровень содержит вдвое больше узлов, чем уровень, расположенный над ним.

Каждый узел в двоичном дереве поиска сам является корнем узлов, исходящих из него, что превращает этот узел и его потомков в поддерево.

Расширенное представление данных 765