Стивен Прата - Язык программирования C. Лекции и упражнения (6-е изд.) 2015

Например, на рис. 17.12 узлы, содержащие слова fate, carpet и llama, образуют левое поддерево всего дерева, а слово voyage является правым поддеревом поддерева style- plmum-voyage.

Предположим, что в таком дереве необходимо найти элемент — назовем его целевым. Если элемент предшествует корневому элементу, поиск понадобится выполнять только в левой половине дерева. Если же целевой элемент следует за корневым элементом, то поиск должен выполняться только в правом поддереве корневого узла. Таким образом, одно сравнение исключает из поиска половину дерева.

Предположим, что поиск осуществляется в левой половине. Это означает сравнение целевого элемента с элементом в левом дочернем узле. Если целевой элемент предшествует элементу левого дочернего узла, то поиск необходимо выполнять только в левой половине дочерних узлов и т.д. Как и при двоичном поиске, каждое сравнение уменьшает количество потенциальных сопоставлений в два раза.

Давайте применим этот метод, чтобы выяснить, присутствует ли слово рирру в дереве, показанном на рис. 17.12. Сравнивая слово puppy с melon (элементом корневого узла) мы видим, что слово puppy, если оно присутствует, должно располагаться в правой половине дерева. Поэтому мы переходим к правому дочернему узлу корневого узла и сравниваем puppy со словом style. В данном случае целевой элемент предшествует элементу узла, поэтому следует двигаться по связи к левому узлу. Здесь находится слово plenum, которое предшествует слову puppy. Теперь необходимо следовать правой ветвью для этого узла, но она пуста. Таким образом, три операции сравнения позволили установить, что слово puppy в дереве отсутствует.

Таким образом, двоичное дерево поиска сочетает преимущества связной структуры с эффективностью двоичного поиска. С точки зрения программирования реализация дерева является более трудоемким процессом, чем создание связного списка. Далее мы построим двоичное дерево для финального проекта ADT.

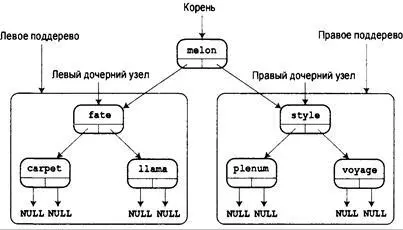
Рис. 17.12. Хранение слов в двоичном дереве поиекп

Создание абстрактного типа данных для двоичного дерева

Как обычно, мы начнем с общего определения двоичного дерева. Это конкретное определение предполагает, что дерево не содержит дублированных элементов. Многие его операции совпадают с операциями со списками. Различие состоит в иерархической организации данных.

766 глава 17

Неформальное определение этого типа ADT выглядит следующим образом.

Имя типа: Двоичное дерево поиска

Свойства типа: Двоичное дерево является либо пустым набором узлов (пустое дерево), либо набором узлов, один из которых обозначает корень. Каждый узел имеет в точности два исходящих из него дерева, называемые левым поддеревом и правым поддеревом.

Каждое поддерево само является двоичным деревом, включая возможность быть пустым деревом.

Двоичное дерево поиска — это упорядоченное двоичное дерево, где каждый узел содержит элемент, внутри которого все элементы в левом поддереве предшествуют корневому элементу, а корневой элемент предшествует всем элементам в правом поддереве.

Операции типа: Инициализация дерева пустым значением Определение, является ли дерево пустым Определение, является ли дерево полным Определение количества элементов в дереве Добавление элемента в дерево Удаление элемента из дерева Поиск элемента в дереве Посещение каждого элемента в дереве Опустошение дерева

Интерфейс двоичного дерева поиска

В принципе, двоичное дерево поиска можно реализовать разнообразными способами. Его можно реализовать даже в виде массива, соответствующим образом манипулируя индексами массива. Но наиболее прямолинейный способ реализации двоичного дерева поиска предполагает использование динамически выделяемых узлов, связанных между собой посредством указателей, так что давайте начнем с определений вроде показанных ниже:

typedef SOMETHING Item;

typedef struct trnode {

Item item;

struct trnode * left; struct trnode * right;

} Trn;

typedef struct tree {

Trnode * root; int size;

} Tree;

Каждый узел содержит элемент, указатель на левый дочерний узел и указатель на правый дочерний узел. Структуру Tree можно было бы определить как тип указателя на Trnode, поскольку для доступа ко всему дереву достаточно знать только местоположение корневого узла. Однако применение структуры с членом size упрощает отслеживание размера дерева.

Расширенное представление данных 767

Мы разработаем программу для ведения реестра домашних животных в клубе Nelville Pet Club, причем каждый элемент будет состоять из клички животного и его вида. Учитывая это, мы можем определить интерфейс, показанный в листинге 17.10. Мы ограничили размер дерева до 10. Небольшой размер облегчает тестирование программы при заполнении дерева. При необходимости значение MAX ITEMS всегда можно увеличить.

Листинг 17.10. Заголовочный файл tree.h для интерфейса двоичного дерева поиска

768 Глава 17

Реализация двоичного дерева

Теперь приступим к реализации множества функций, описанных в файле tree.li. Функции InitializeTree(), EmptyTree(), FullTree() и Treeltems() достаточно просты и работают подобно своим аналогам в абстрактных типах данных списка и очереди, поэтому мы уделим основное внимание остальным функциям.

Добавление элемента

При добавлении элемента в дерево сначала потребуется проверить, есть ли место для нового узла. Поскольку двоичное дерево поиска определено так, что не может содержать дублированных элементов, далее необходимо выяснить, не присутствует ли данный элемент в дереве. Если новый элемент удовлетворяет этим двум начальным условиям, нужно создать новый узел, скопировать в него элемент и установить левый и правый указатели узла в NULL. Это говорит об отсутствии дочерних узлов у дочернего узла. Затем следует обновить элемент size структуры Tree с целью отражения добавления нового элемента. Далее понадобится выяснить, в какую позицию дерева должен быть помещен новый узел. Если дерево пустое, корневой указатель необходимо установить так, чтобы он ссылался на новый узел. В противном случае потребуется просмотреть дерево, чтобы найти в нем место для добавления узла. Функция Addltem() выполняет эти действия, передавая часть работы функциям, которые пока еще не определены: Seekltem(), MakeNode() и AddNode().

Расширенное представление данных 769