Стивен Прата - Язык программирования C. Лекции и упражнения (6-е изд.) 2015

Стандарт C11 посредством библиотеки uchar.h предоставляет функции для преобразования между многобайтным представлением и представлением charl6_t, а также между многобайтным представлением и представлением char32_t.

Раздел VIII. Расширенные вычислительные средства С99/С11

Исторически сложилось так, что первым языком для выполнения числовых научных и инженерных вычислений был FORTRAN. Стандарт С90 привел методы вычислений С в более полное соответствие с FORTRAN. Например, спецификация характеристик плавающей запятой, использованная в float.h, основана на модели, которая разработана комитетом по стандартизации FORTRAN. В стандартах С99 и С11 продолжена работа по расширению пригодности языка С к решению вычислительных задач. Например, массивы переменной длины, добавленные в С99, но сделанные необязательными в С11, в большей степени соответствуют стилю применения массивов FORTRAN, чем традиционные массивы С. (В СИ определен макрос

__ STDC_N0_VLA_ , который развертывается в 1, если реализация не поддерживает

массивы переменной длины.)

Стандарт плавающей запятой IEC

Международная электротехническая комиссия (IEC) опубликовала стандарт вычислений с плавающей запятой (IEC 60559). Этот стандарт включает описание форматов плавающей запятой, точности, представления NaN, бесконечности, методик округления, преобразований, исключений, рекомендованных функций и алгоритмов и тому подобного. В С99 этот стандарт был принят как руководство по реализации вычислений с плавающей запятой на языке С. Большая часть дополнений С99, касающихся средств работы с плавающей запятой, являются частью этих усилий. Речь идет о таких вещах, как заголовочный файл fenv.h и некоторые из новых математических функций. Кроме того, в заголовочном файле float.h определено несколько макросов, имеющих отношение к модели плавающей запятой IEC.

904 Приложение Б

Модель плавающей запятой

Давайте вкратце рассмотрим модель плавающей запятой. Стандарт представляет значение с плавающей запятой х как степень основания системы счисления, умноженная на дробную часть, которая представлена в этой системе счисления, в отличие от экспоненциальной формы записи языка С, где мы можем записать 876.54 в виде 0.87654ЕЗ. Как и можно было ожидать, формальное представление выглядит более внушительно:

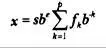
Выражаясь кратко, эта формула представляет число как результат умножения показателя степени, или экспоненты (е), основания системы счисления (b) на значащую часть числа, т.е. многозначную дробную часть.

Ниже описаны различные компоненты формального представления.

• s — знак (±1).

• b — это основание системы счисления. Наиболее распространенным значением является 2, т.к. в процессорах с плавающей запятой обычно применяется двоичная арифметика.

• e представляет целочисленную экспоненту. (Ее не следует путать с числовой константой е, используемой в качестве основания для натуральных логарифмов.) Экспонента будет ограничена диапазоном, имеющим минимальное и максимальное значение. Эти значения будут зависеть от количества битов, выделенных для хранения экспоненты.

• f kпредставляет возможные цифры для основания системы счисления б, например, при основании 2 возможными цифрами являются 0 и 1, а при основании 16 — цифры из диапазона от 0 до F.

• р — это точность, т.е. количество цифр по основаниюb, применяемых для представления значащей части числа. Значение р будет ограничено количеством битов, выделенных для хранения значащей части числа.

Понимание этого представления является ключом к пониманию содержимого float.h и fenv.h, поэтому давайте ознакомимся с двумя примерами, иллюстрирующими работу представления плавающей запятой.

Прежде всего, предположим, что основанием системы счисления б является 10, а точность р составляет 5. Тогда значение 24,51 можно было бы записать следующим образом:

(+1)10^(2/10 + 4/100 + 5/1000 + 1/10000 + 0/100000)

Полагая, что компьютер способен хранить десятичные цифры, он мог бы сохранить знак, экспоненту 3, а также пять значений f k— 2, 4, 5, 1 и 0. (Здесь f 1— это 2, f 2- 4 и т.д.) Таким образом, значащей частью является 0.24510. Умножение ее на 10 3дает 24.51.

Далее предположим, как более распространенную ситуацию, что основание системы счисления b представляет собой 2. Пусть р равно 7, экспонента равна 5, а значащая часть числа хранится как 1011001, используя 7 двоичных цифр, как описано посредством р. Будем считать, что знак числа положителен.

Справочные материалы 905

Тогда согласно формуле мы можем построить число так:

х= (+1 )2 5( 1/2 +0/4 + 1/8 + 1/16 + 0/32 + 0/64 + 1/128)

= 32( 1/2 +0/4 + 1/8 + 1/16 + 0/32 + 0/64 + 1/128)

= 16 + 0 + 4 + 2 +0 + 0 + 1/4 = 22.25

Многие макросы из float.h имеют отношение к этому представлению. Например, для значения типа float макрос FLT_RADIX — это b, т.е. применяемое основание системы счисления, a FLT_MANT_DIG — это р, т.е. количество цифр (по основанию b) в значащей части числа.

Нормальные и субнормальные значения

Концепция нормалшованного значения с плавающей запятой играет важную роль, поэтому давайте изучим ее. Для простоты предположим, что основанием системы счисления является 10 (b = FLT_RADIX = 10), а в значащей части числа используется 5 десятичных цифр для значения типа float (р = FLT_MANT_DIG = 5). (Стандарт требует более высокой точности, чем эта, но желание упростить изучение позволяет нам проигнорировать данное требование.) Взгляните на следующие способы представления значения 31.841:

экспонента = 3, значащая часть = .31841 (.31841E3) экспонента = 4, значащая часть = .03184 (.03184Е4) экспонента = 5, значащая часть = .00318 (.00318Е5)

Очевидно, что первый метод будет наиболее точным, поскольку в значащей части присутствуют все пять доступных цифр. Нормализованное ненулевое значение с плавающей запятой — это такое значение, в котором первая цифра в значащей части отличается от нуля, и именно так обычно хранятся значения с плавающей запятой.

Теперь предположим, что минимальная экспонента (FLT_MIN_EXP) установлена в -10. Тогда наименьшее нормализованное значение таково:

экспонента = -10, значащая часть = .10000 (.10000Е-10)

Обычно умножение или деление на 10 означает увеличение или уменьшение экспоненты, но в этом случае деление не может дополнительно уменьшить экспоненту. Однако можно изменить значащую часть, чтобы получить следующее представление:

экспонента = -10, значащая часть = 0.0100 (.01000Е-10)

Такое число будет называться субнормальным, потому что оно не использует полную точность значащей части. Например, деление 0.12343Е-10 на 10 дает .01234Е-10, и одна цифра теряется.

В данном примере 0.1000Е-10 является наименьшим ненулевым нормальным представлением (FLT_MIN), а наименьшим ненулевым субнормальным значением будет 0.00001Е-10 (FLT_TRUE_MIN).