Эндрю Уэзеролл - Компьютерные сети. 5-е издание

5.2.2. Алгоритм нахождения кратчайшего пути

Начнем наше изучение алгоритмов выбора маршрутов с простого метода вычисления кратчайших путей, требующего полной информации о сети. Целью распределенного алгоритма является нахождение таких путей даже в тех случаях, когда маршрутизатор не располагает всеми сведениями о сети.

Идея заключается в построении графа сети, в котором каждый узел будет соответствовать маршрутизатору, а каждое ребро — линии связи или просто связи. При выборе маршрута между двумя маршрутизаторами алгоритм просто находит кратчайший путь между ними на графе.

Концепция кратчайшего пути( shortest path) требует некоторого пояснения. Один из способов измерения длины пути состоит в подсчете количества транзитных участков. В таком случае пути ABC и ABE на рис. 5.6 имеют одинаковую длину. Можно измерять расстояния в километрах. В таком случае окажется, что путь ABC значительно длиннее пути ABE (предполагается, что рисунок изображен с соблюдением масштаба).

Однако, помимо учета количества транзитных участков и физической длины линий, возможен учет и других параметров. Например, каждому ребру графа можно поставить в соответствие среднее время задержки стандартного тестового пакета, измеряемое каждый час. В таком графе кратчайший путь определяется как самый быстрый путь, а не путь с наименьшим числом ребер или наименьшей длиной в километрах.

В общем случае параметры ребер графа являются функциями расстояния, пропускной способности, средней загруженности, стоимости связи, измеренной величины задержки и других факторов. Изменяя весовую функцию, алгоритм может вычислять кратчайший путь с учетом любого количества критериев в различных комбинациях.

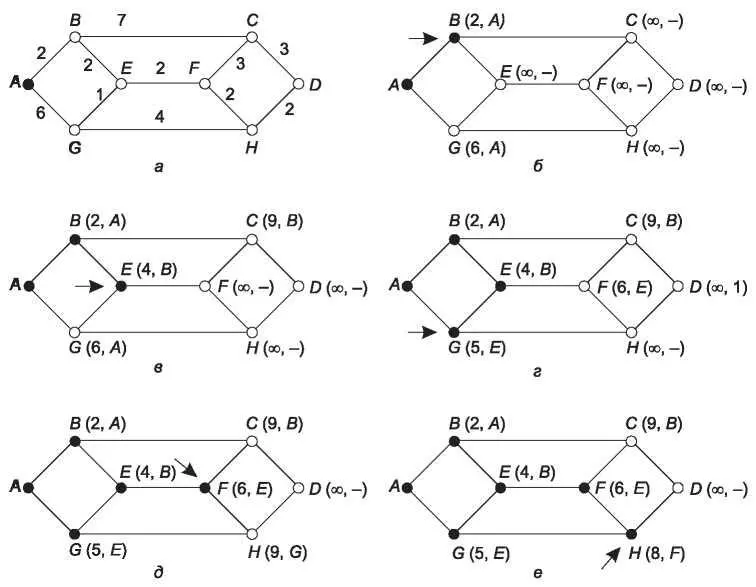
Рис. 5.6.Первые шесть шагов вычисления кратчайшего пути от A к D. Стрелка указывает на рабочий узел

Известно несколько алгоритмов вычисления кратчайшего пути между двумя узлами графа. Один из них был создан знаменитым Дейкстрой (Dijkstra) в 1959 году. Он находит кратчайшие пути между отправителем и всеми возможными адресами назначения в данной сети. Каждый узел помечается (в скобках) расстоянием до него от узла отправителя по наилучшему известному пути. Эти расстояния должны быть неотрицательными; если они основаны на реальных величинах — таких как пропускная способность и время задержки, — это условие будет выполнено. Вначале пути неизвестны, поэтому все узлы помечаются символом бесконечности. По мере работы алгоритма и нахождения путей отметки узлов изменяются, показывая оптимальные пути. Отметка может быть постоянной или экспериментальной. Вначале все отметки являются ориентировочными. Когда выясняется, что отметка действительно соответствует кратчайшему возможному пути, она становится постоянной и в дальнейшем не изменяется.

Чтобы показать, как работает этот алгоритм, рассмотрим взвешенный ненаправленный граф на рис. 5.6, а, где весовые коэффициенты соответствуют, например, расстояниям. Мы хотим найти кратчайший путь от A к D. Для начала мы черным кружком помечаем узел A как постоянный. Затем мы исследуем все соседние с ним узлы, указывая около них расстояние до узла A. Если отыскивается более короткий путь к какому-либо узлу, то вместе с указанием расстояния в отметке меняется и узел, через который прошел более короткий путь. Таким образом, позднее можно восстановить весь путь. Если бы в сети было более одного кратчайшего пути от A до D и мы хотели бы найти их все, нам нужно было бы запоминать все узлы, которые позволяют дойти до данного узла, пройдя одинаковое расстояние.

Рассмотрев все соседние с A узлы, мы помечаем ближайший узел как постоянный, как показано на рис. 5.6, б. Этот узел становится новым рабочим узлом.

Теперь мы повторяем ту же процедуру с узлом B, исследуя все его соседние узлы. Если сумма расстояния от узла B и значения отметки в узле B (расстояния от A до B) оказывается меньше, чем отметка у исследуемого узла (уже найденное другим путем расстояние от A), это значит, что найден более короткий путь, поэтому пометка узла изменяется.

После того как все соседние с рабочим узлы исследованы и временные отметки при необходимости изменены, по всему графу ищется узел с наименьшей временной отметкой. Этот узел помечается как постоянный и становится текущим рабочим узлом. На рис. 5.6 показаны первые шесть этапов работы алгоритма.

Чтобы понять, как работает алгоритм, посмотрим на рис. 5.6, в. На данном этапе узел E только что был отмечен как постоянный. Предположим, что существует более короткий путь, нежели ABE, например AXYZE (для некоторых X и Y ). В этом случае есть две возможности — либо узел Z уже сделан постоянным, либо еще нет. Если да, значит, узел E уже проверялся, когда узел Z был сделан постоянным и, следовательно, рабочим узлом. В этом случае путь AXYZE уже исследовался.

Теперь рассмотрим случай, когда узел Z все еще помечен как временный. Если отметка узла Z больше или равна пометки узла E, путь AXYZE не может быть короче, чем путь ABE. Если же отметка узла Z меньше пометки узла E, то тогда узел Z должен был стать постоянным раньше узла E, и узел E проверялся бы с узла Z.

Этот алгоритм приведен в листинге 5.1. Глобальные переменные n и dist описывают граф и инициализируются раньше, чем вызывается shortest_path. Единственное отличие программы от описанного выше алгоритма заключается в том, что вычисление кратчайшего пути в программе начинается не от узла-источника s, а от конечного узла t.

Поскольку в однонаправленном графе кратчайшие пути от t к s те же самые, что и от s к t, не имеет значения, с какого конца начинать. Причина поиска пути в обратном направлении заключается в том, что каждый узел помечается предшествующим узлом, а не следующим. Когда найденный путь копируется в выходную переменную path, он инвертируется. В результате двух инверсий мы получаем путь, идущий в нужную сторону.

Листинг 5.1.Алгоритм Дейкстры вычисления кратчайшего пути по графу

Листинг 3.7 (продолжение)

5.2.3. Заливка

При реализации алгоритма маршрутизации любой маршрутизатор должен принимать решения на основании локальных сведений, а не полной информации о сети. Одним из простых локальных методов является заливка( flooding), при которой каждый приходящий пакет посылается на все исходящие линии, кроме той, по которой он пришел.