Эндрю Уэзеролл - Компьютерные сети. 5-е издание

Процесс обновления таблицы проиллюстрирован на рис. 5.7. На рис. 5.7, а показана сеть. Первые четыре столбца на рис. 5.7, б показывают векторы задержек, полученные маршрутизатором J от своих соседей. Маршрутизатор A считает, что время пересылки от него до маршрутизатора B равно 12 мс, 25 мс до маршрутизатора C, 40 мс до D и т. д. Предположим, что маршрутизатор J измерил или оценил задержки до своих соседей A, I, H и K как 8, 10, 12 и 6 мс соответственно.

Теперь рассмотрим, как J рассчитывает свой новый маршрут к маршрутизатору G. Он знает, что задержка до A составляет 8 мс и при этом A думает, что от него до G данные дойдут за 18 мс. Таким образом, J знает, что если он станет отправлять пакеты для G через A, то задержка составит 26 мс. Аналогично, он вычисляет значения задержек для маршрутов от него до G, проходящих через остальных его соседей (I, H и K), и получает соответственно 41 (31 + 10), 18 (6+12) и 37 (31+6). Лучшим значением является 18, поэтому именно оно помещается в таблицу в запись для получателя G. Вместе с числом 18 туда же помещается обозначение линии, по которой

проходит самый короткий маршрут до G, то есть H. Данный метод повторяется для всех остальных адресатов, и при этом получается новая таблица, показанная в виде правого столбца на рисунке.

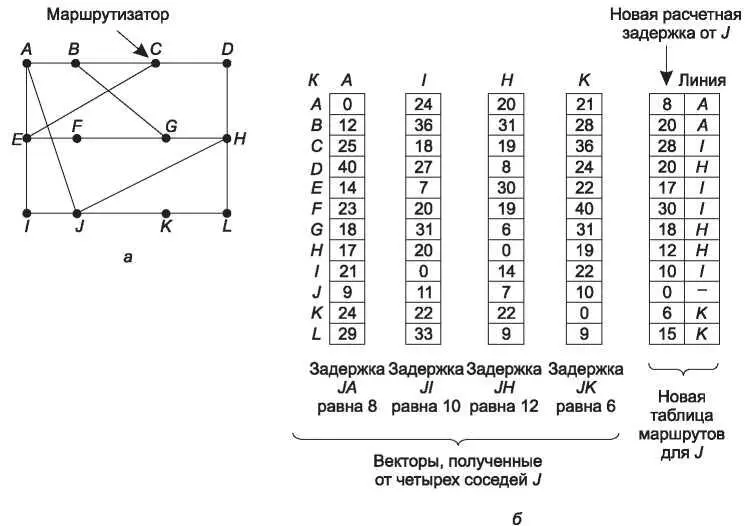
Рис. 5.7. Сеть (а); полученные от A, I, H и K векторы и новая таблица маршрутов для J (б)

Проблема счета до бесконечности

Установление маршрутов, соответствующих кратчайшим путям, в сети называется конвергенцией( convergence). Алгоритм маршрутизации по вектору расстояний — простой метод, позволяющий маршрутизаторам совместно вычислять кратчайшие пути. Однако на практике он обладает серьезным недостатком: хотя правильный ответ в конце концов и находится, процесс его поиска может занять довольно много времени. В частности, такой алгоритм быстро реагирует на хорошие новости и очень лениво — на плохие. Рассмотрим маршрутизатор, для которого расстояние до маршрутизатора X достаточно велико. Если при очередном обмене векторами его сосед A сообщит ему, что от него до маршрутизатора X совсем недалеко, наш маршрутизатор просто переключится для передач маршрутизатору X на линию, проходящую через этого соседа. Таким образом, хорошая новость распространилась всего за один обмен информацией.

Чтобы увидеть, как быстро распространяются хорошие известия, рассмотрим линейную сеть из пяти узлов, показанную на рис. 5.8, в которой мерой расстояния служит количество транзитных участков. Предположим, что вначале маршрутизатор A выключен, и все остальные маршрутизаторы об этом знают. То есть они считают, что расстояние до A равно бесконечности.

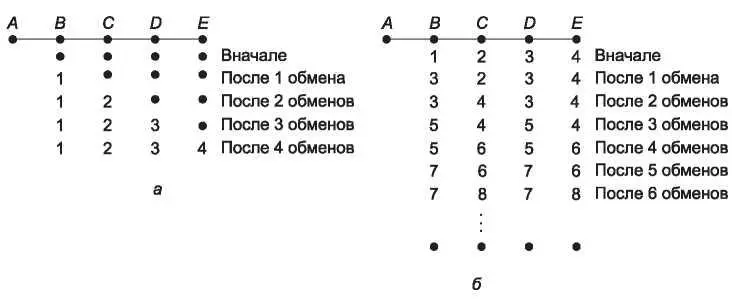
Рис. 5.8. Проблема счета до бесконечности

Когда в сети появляется A, остальные маршрутизаторы узнают об этом с помощью обмена векторами. Для простоты будем предполагать, что где-то в сети имеется гигантский гонг, в который периодически ударяют, чтобы инициировать одновременный обмен векторами. После первого обмена B узнает, что у его соседа слева нулевая задержка при связи с A, а B помечает в своей таблице маршрутов, что A находится слева на расстоянии одного транзитного участка. Все остальные маршрутизаторы в этот момент еще полагают, что A выключен. Значения задержек для A в таблицах на этот момент показаны во второй строке на рис. 5.8, а. При следующем обмене информацией C узнает, что у B есть путь к A длиной 1, поэтому он обновляет свою таблицу, указывая длину пути до A, равную 2, но D и E об этом еще не знают. Таким образом, хорошие вести распространяются со скоростью один транзитный участок за один обмен векторами. Если самый длинный путь в сети состоит из N транзитных участков, то через N обменов все маршрутизаторы подсети будут знать о включенных маршрутизаторах и заработавших линиях.

Теперь рассмотрим ситуацию на рис. 5.8, б, в которой все связи и маршрутизаторы изначально находятся во включенном состоянии. Маршрутизаторы B, C, D и E находятся на расстоянии 1, 2, 3 и 4 транзитных участков от A соответственно. Внезапно либо A отключается, либо происходит обрыв линии между A и B (что с точки зрения B одно и то же).

При первом обмене пакетами B не слышит ответа от A. К счастью, C говорит: «Не волнуйся. У меня есть путь к A длиной 2». B вряд ли догадывается, что путь от C к A проходит через B. B может только предполагать, что у C около 10 выходных связей с независимыми путями к A, кратчайшая из которых имеет длину 2. Поэтому теперь B думает, что может связаться с A через C по пути длиной 3. При этом первом обмене маршрутизаторы D и E не обновляют свою информацию об A.

При втором обмене векторами C замечает, что у всех его соседей есть путь к A длиной 3. Он выбирает один из них случайным образом и устанавливает свое расстояние до A равным 4, как показано в третьей строке на рис. 5.8, б. Результаты последующих обменов векторами также показаны на этом рисунке.

Теперь должно быть понятно, почему плохие новости медленно распространяются — ни один маршрутизатор не может установить значение расстояния, более чем на

единицу превышающее минимальное значение этого расстояния, хранящееся у его соседей. Таким образом, все маршрутизаторы будут до бесконечности увеличивать значение расстояния до выключенного маршрутизатора. Количество необходимых для завершения этого процесса обменов векторами можно ограничить, если установить значение этой «бесконечности» равным длине самого длинного пути плюс 1.

Неудивительно, что эта проблема называется счетом до бесконечности (count-to-infinity). Было сделано много попыток решить ее, например можно запретить маршрутизатору сообщать о своих кратчайших путях соседям, от которых они получили эту информацию, с помощью правила расколотого горизонта с «отравляющим» ответом внесенного в RFC 1058. Однако на практике все эти эвристические правила с красивыми названиями оказались абсолютно бесполезными. Суть проблемы заключается в том, что когда Х сообщает Y о том, что у него есть какой-то путь, у Y нет никакой возможности узнать, входит ли он сам в этот путь.