Юрченко Борисович - Философия и логика времени

Речь здесь даже не идет о той фантастической истории, в которой кто-то может убить случайно своего предка, сделав невозможным собственное бытие. Временная петля подразумевает, что в какой-то момент время должно остановиться и пойти вспять. Такая точка остановки согласно лемме 2 становится точкой коллапса Вселенной. Иначе говоря, если бы библейскому персонажу Навину действительно удалось бы остановить время, он получил бы самое мощное оружие в истории человечества, позволяющее уничтожить всю Вселенную или, по крайней мере, некоторую окрестность в ней. Что касается сверхсветовой скорости, то это предполагает обратную стрелу времени, для которой нужна другая Вселенная, но не эта. Говорить о ней в нашей Вселенной бессмысленно.

Что есть мгновение? Математическое мгновение – это небольшой интервал времени, в пределе равный бесконечно малой величине. Логика, по которой мы мыслим, используется нами как вневременная. Мы выстраиваем силлогизм и говорим, что из идеи А следует идея В, не предполагая временной процесс между ними. Но точно также мы говорим, что из физического события А следует физическое событие В . А это уже требует времени. Следовательно, эти события должны быть разделены временем, а значит, находиться в разных стратах факторизованного пространства M/t. (рис.2) .

В традиционном определении причинного множества в М используется бинарное отношение , обладающее свойствами:

(1) транзитивности:

(2) иррефлексивности:

(3) локальности:

где «card» означает мощность множества, которая не может быть бесконечной [12,13].

Отношение причинности является временным. Отсюда автоматически следует, что причинное множество должно быть дискретным, а любая его причинная (Марковская) цепь – вполне упорядоченной и конечной, т.е. счетной, в которой, кроме того, невозможны циклы, так чтобы никакое событие не могло оказаться причиной самого себя:

(2.3)

В этом случае в световом конусе должна возникать временная петля, а это значит, что некоторые события в этой цепи обращают время вспять. В пространства M/t эти события должны оказаться в нижних стратах, т.е. в предыдущих состояниях Вселенной, но мы уже пришли к выводу, что в такой модели вообще ничего не может происходить, никакой причинности. Отсутствие временных петель является обязательным для релятивизма.

III. Исчисляемое время и континуум

Реальный континуум не дан нам в практическом опыте, но существует только как математическая абстракция (связное компактное Хаусдорфово пространство). Согласно аксиоме Дедекинда, существует взаимно однозначное соответствие между действительными числами и точками прямой. Действительные числа – это все целые числа вида n , рациональные (дроби целых чисел вида n/k ) и иррациональные числа (бесконечные десятичные дроби как, например, числа Пифагора π или Непера е ). На прямой действительные числа признаются точками, которые являются бесконечно малыми величинами – дифференциалами. В таком определении континуум невозможно рассечь на два непересекающихся подмножества, чтобы между ними ничего не осталось: сечение либо принадлежит обоим частям, либо оказывается не охвачено ни одним из них. Через определение предела задаются правила дифференцирования и интегрирования для действительных (и комплексных) функций. Но континуум С «больше» счетного множества. Кантор указал простой алгоритм, по которому все рациональные числа (включая и целые) можно пересчитать, выстроив их в бесконечную таблицу:

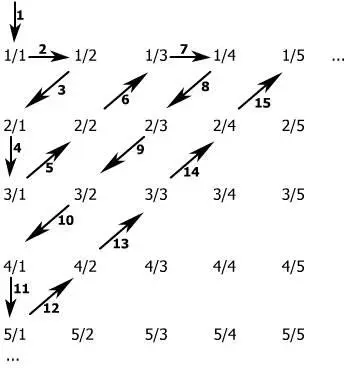
Рис. 5

Это позволило ему определить единую счетную мощность для всех бесконечных дискретных множеств. А затем Кантор с помощью своего диагонального метода (который Гедель использовал для своей теоремы о неполноте) показал, что континуум невозможно пересчитать. Остановимся на этом результате, поскольку структура континуума прямо связана с нашими представлениями о причинности и тем, что мы считаем мгновением (настоящим), которое в свою очередь связано со скоростью света. В самой общей форме это выглядит так. Допустим, что множество всех действительных (рациональных и иррациональных) чисел не более чем счетно. Впрочем, достаточно будет ограничиться множеством всех этих чисел на отрезке от 0 до 1 (можно показать, что достаточно даже 1/10, 1/100, 1/1000… части отрезка), так что каждое рассматриваемое нами число будет десятичной дробью вида 0,1234…890…, в которой цифры комбинируются всеми возможными способами. Если их можно упорядочить (с помощью аксиомы выбора), т.е. пересчитать, как и все рациональные числа, то это значило бы, что континуум счетен (т.е. дискретен). Но затем Кантор показал, как получить число, которого нет в этом списке. Допустим, что все действительные числа можно пересчитать. Выстроим их в столбец.

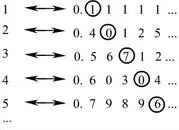
Рис. 6

Новое число составим так. Двигаясь по диагонали от числа к числу, будем вписывать в новое число 0, если видим любую другую цифру от 1 до 9, а если видим 0, то пишем 1. Полученное число будет выглядеть так же, как и все остальные, но при этом оно будет отличаться от каждого из них по крайней мере в одном знаке. А значит, такого числа не могло быть в списке изначально. Следовательно, континуум С невозможно пересчитать, приписав ему мощность . Отсюда Кантор высказал свою континуум-гипотезу (СН), которую Гильберт поставил на первое место в своих знаменитых проблемах. Ее смысл заключался в том, что между счетностью (дискретностью) и несчетностью (континуальностью) нет промежуточных мощностей, а значит, между ними невозможно установить изоморфизм, невозможно редуцировать континуум С до N.

Обратим внимание на то, что в таком понимании континуума несчетность оказывается синонимом неупорядоченности: если С невозможно упорядочить – значит, его мощность превосходит счетную. Но по сути уже пересчет рациональных чисел создает хаос: их номера в пересчете по n будут, конечно, иметь естественный порядок следования <, но сами рациональные числа окажутся в разбросе. Если при этом мы полагаем, что процесс их создания в континууме должен быть последовательным, то пересчет Кантора никуда не годится. Он лишает континуум порядка уже на уровне рациональных чисел.

Лемма3. Несчетность = Неупорядоченность

Фактически именно это и доказал Кантор. За изначально постулированный порядок в С несет ответственность аксиома выбора (АС). Она утверждает, что в любом множестве можно выбрать любую точку, не предлагая конструктивной процедуры, кроме одной – ткнуть пальцем. И поэтому последовательным случайным перебором можно исчерпать любое множество. Искусственность этой аксиомы вызвала у многих математиков сомнения в ее правомочности, хотя законов дедукции АС не нарушает. Так или иначе, мы ведь тоже убеждены, что можем своим умом локализовать любую точку в прошлом или будущем. Что нам мешает мысленно заглянуть в Юрский период или в сингулярность Большого взрыва? Или хотя бы в завтрашний день, который мы себе уже заранее расписали по часам и даже минутам?