Ричард Фейнман - 1. Современная наука о природе, законы механики

Е=q 1r/4pe 0r 3. (12.4)

А затем мы пишем

F=q 2 E, (12.5)

т. е. связываем силу, поле и заряд в поле. В чем же суть всего этого? Суть в том, что анализ разделяется на две части. Одна часть говорит, что что-то создает поле, а другая — что оно дей­ствует на что-то. Позволяя нам рассматривать две части не­зависимо, это разделение упрощает во многих случаях расчеты трудных задач. Когда зарядов много, то сперва мы рассчиты­ваем суммарное электрическое поле, создаваемое этими заря­дами в R, а потом, зная величину заряда, помещенного в R, находим силу, действующую на него.

Да и в случае тяготения мы можем сделать то же самое. Сила теперь F =-Gm 1 m z r/r 3 . Анализ полностью совпадает: сила притяжения тела в поле тяготения равна произведению массы тела на поле С. Сила, действующая на m 2 , равна массе т 2 , умноженной на поле С. созданное массой m 1 , т. е. F= m 2C. Значит, поле С, создаваемое массой m 1, есть С=- Gm 1 r/r 3 ; оно, как и электрическое поле, направлено по радиусу.

Такое разделение на две части не так уж тривиально, как могло бы показаться на первый взгляд. Оно было бы триви­альным, было бы просто иной записью того же самого, если бы законы действия сил были совсем просты, но они очень сложны, и оказывается, что поле настолько реально, что почти не зави­сит от объектов, создающих его. Можно колебать заряд, и влияние этого (поле) скажется на расстоянии. Если колебания прекратятся, в поле все равно будут ощущаться следы этих колебаний, потому что взаимодействие двух частиц не про­исходит мгновенно. Оттого и желательно уметь запоминать, что здесь раньше происходило. Если сила действия на заряд зави­сит от того, где другой заряд был вчера и каким он тогда был, то должна быть возможность проследить за тем, что было вчера; в этом и состоит сущность поля. Чем сложнее силы, тем реаль­ней поле, и наша техника разделения становится все менее и менее искусственной.

Желая анализировать силы при помощи полей, мы нуж­даемся в законах двоякого рода. Первые—это отклик на поле. Они дают нам уравнения движения. Например, закон отклика массы на поле тяжести состоит в том, что сила равна массе, умноженной на поле тяжести, или если тело еще и заряжено, то отклик заряда на электрическое поле равен заряду, умно­женному на электрическое поле. Вторая часть анализа природы в таких положениях — это формулировка законов, определяющих напряженность поля и способ его возникновения. Эти за­коны иногда называют уравнениями поля, В нужный момент мы с ними познакомимся, а пока скажем о них лишь несколько

слов.

Вот вам для начала самое замечательное свойство поля, оно абсолютно точно и легко усваивается. Общее электрическое по­ле, создаваемое группой источников, есть векторная сумма полей, создаваемых по отдельности первым, вторым и т. д. источ­никами. Иными словами, когда поле создано множеством заря­дов и если отдельное поле первого есть Е 1, а второго — Е 2 и т. д., то мы должны просто сложить эти векторы, чтобы полу­чить общее поле. Принцип этот выражается в виде

Е= Е 1+ Е 2 + Е 3 + ... (12.6) или, в согласии с определением поля,

Можно ли эти методы применить к тяготению? Силу притя­жения двух масс m 1и m 2 Ньютон выразил в виде F=- Gm 1 m 2 r/r 3 . Но в соответствии с понятием поля можно ска­зать, что m 1создает поле С во всем окружающем пространстве и сила, притягивающая m 2, равна

F= m 2 C. (12.8)

По аналогии с электричеством

и тогда поле тяжести нескольких масс равно

С= С 1 + С 2 + С 3 +.. . (12.10)

В гл. 7, где рассматривалось движение планет, мы по существу использовали именно этот принцип. Мы складывали все векто­ры сил, чтобы обнаружить общую силу, действующую на пла­нету. Разделив на ее массу, мы и получим (12.10).

Уравнения (12.6) и (12.10) выражают так называемый прин­цип суперпозиции, или наложения полей. Этот принцип про­возглашает, что общее поле нескольких источников есть сумма полей, создаваемых каждым из них. Насколько нам ныне известно, закон этот в электричестве наверняка выполняется даже тогда, когда заряды движутся и закон сил усложняется. Бывают иногда кажущиеся нарушения, но внимательный анализ всегда доказывает, что просто забыли какой-нибудь из движущихся зарядов. Но в отличие от электрических зарядов для сильных полей тяжести он не совсем точен. В теории тяготения Эйнштейна доказывается, что уравнение Ньютона (12.10) соблюдается лишь приближенно.

С электричеством тесно связана сила другого рода, назы­ваемая магнитной; ее тоже можно анализировать через поня­тие поля. Некоторые из качественных связей между этими си­лами видны в опыте с электронной трубкой (фиг. 12.3).

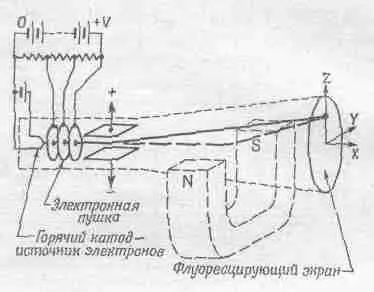
Фиг. 12.3. Электронная трубка.

На одном конце трубки помещен источник, испускающий поток элект­ронов, а внутри имеется устройство, разгоняющее электроны до большой скорости и посылающее часть их на светящийся экран на другом конце трубки. Световое пятно в центре экра­на, в месте ударов электронов, позволяет проследить за их путем. На пути к экрану пучок проходит сквозь узкую щель между параллельными металлическими пластинами, располо­женными, допустим, плашмя. К пластинам подведено напря­жение, позволяющее любую из них заряжать отрицательно. Напряжение создает между пластинами электрическое поле.

В первой части опыта отрицательное напряжение подается на нижнюю пластину, т. е. на ней образуется избыток элект­ронов. Одноименные заряды отталкиваются, и поэтому светящее­ся пятно на экране взлетает внезапно вверх. (Можно сказать и иначе: электроны «чувствуют» ноле и отвечают отклоне­нием вверх.) Затем переключим напряжение и зарядим отрица­тельно уже верхнюю пластину. Световое пятно на экране опу­стится вниз, показывая, что электроны пучка отталкиваются электронами верхней пластины. (Иначе говоря, электроны «ответили» на изменение направления поля.)

Во второй части опыта напряжение на пластины уже не подается, а вместо этого проверяется влияние магнитного поля на электронный пучок. Для этого необходим подковообразный магнит, достаточно широкий, чтобы «оседлать» практически всю трубку. Предположим, что мы подвели магнит снизу к трубке, обхватили им ее и направили полюсы кверху (в виде буквы U). Мы замечаем, что пятно на экране смещается, скажем кверху, когда магнит приближается снизу. Выходит, что магнит отталкивает пучок. Но не так все просто: если мы пере­вернем магнит, не переставляя его сторон, и приблизим его к трубке сверху, то пятно снова сдвинется вверх, т. е. вместо оттал­кивания наступило притяжение. А теперь вернем магнит в пер­воначальное положение, когда он обхватывал трубку снизу. Да, пятно по-прежнему отклоняется кверху; но повернем маг­нит на 180° вокруг вертикальной оси, чтобы он имел вид буквы U, но уже с переставленными полюсами. Смотрите-ка, пятно прыгает вниз и остается там, даже если мы переворачиваем те­перь U вверх ногами.