Дуглас Хаббард - Как измерить все, что угодно [Оценка стоимости нематериального в бизнесе]

Мы могли бы начертить на том же графике и другие кривые полезности для инвестиционных проектов с ненулевой ценностью, каждая из которых соответствовала бы некоей полезности. Иногда экономисты называют эти графики кривыми изополезности, подразумевая, что полезность фиксированна, или постоянна. Поскольку человеку безразлично, какую из двух точек на такой кривой выбрать, экономисты также называют кривую полезности кривой безразличия [38] Кривая безразличия — геометрическое место точек, каждая из которых представляет такую комбинацию двух свойств, что пользователю безразлично, какую ему выбрать. Другими словами, кривая безразличия показывает альтернативные сочетания этих свойств, обеспечивающие одинаковый уровень полезности. Двиагясь от одной комбинации к другой, пльзователь увеличивает полезность, обеспечиваемую одним свойством, но уменьшает полезность, обеспечиваемую другим свойством. — Примеч. переводчика. . Аналогично тому, как замкнутые линии на картах рельефа показывают точки, расположенные на одинаковой высоте, кривая полезности — геометрическое место точек, отражающих одинаково ценные комбинации.

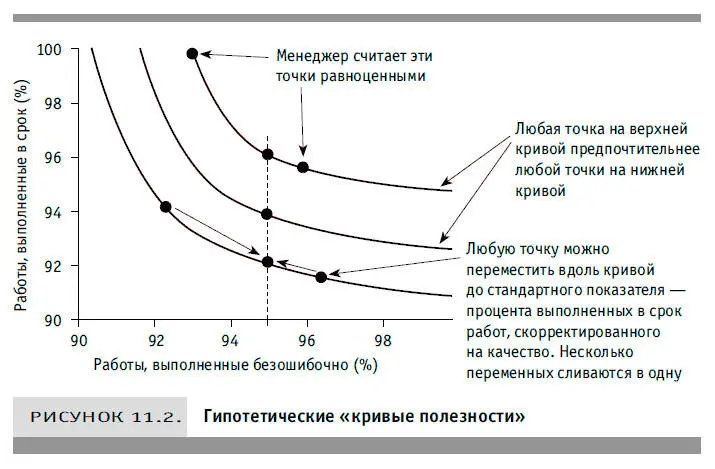
Рисунок 11.2 представляет собой график с несколькими кривыми полезности. Он иллюстрирует гипотетический пример оценки руководством компромиссов между качеством работы и пунктуальностью выполнения заказов. Рисунок помогает внести ясность в требования, предъявляемые программисту, инженеру, редактору и т. д. Вы видите, что если бы сотрудники А и Б выполняли в срок одинаковое число заданий, но А допускал меньше ошибок, то его считали бы лучшим работником. Кривая обосновывает предпочтения, когда выбор не очевиден, например когда качество работы А выше, но Б более пунктуален.

Эти кривые построены таким образом, чтобы любые две точки на каждой из них отражали одинаково ценные комбинации параметров. Так, верхняя кривая показывает, что, по мнению топ-менеджмента, работник, выполняющий на 96 % правильно и на 96 % в срок порученные ему задания, имеет для компании ту же ценность, как тот, кто на 93 % правильно и на 100 % в срок делает свою работу. Не забудьте, что это только гипотетическая оценка какого-то конкретного менеджеpa, а не общепринятая фиксированная норма. Вполне возможно, что ваши предпочтения оказались бы несколько иными.

Было построено семейство аналогичных кривых таким образом, что любая точка на верхней кривой считается более предпочтительной, чем любая точка на нижней. Для сравнения достаточно начертить лишь несколько кривых, хотя на самом деле между приведенными на рисунке линиями существует бесчисленное множество линий. Просто менеджеры строят их ровно столько, сколько нужно для интерполяции.

Кривая полезности, обеспечиваемой любыми двумя факторами (например, качеством работы и ее своевременным выполнением или низким риском и высокой доходностью), позволяет упростить выражение ценности комбинации факторов, представленной точкой на графике. Поскольку каждую точку можно перемещать вдоль кривой так, что ее ценность не изменится, можно рассматривать все точки эквивалентными одной, расположенной на единой стандартизированной линии. В этом случае мы стандартизируем качество и выражаем сравнительную ценность любой точки на графике через коэффициент своевременности выполнения работ, скорректированный на качество. Заявив, что «сотрудник, выполняющий безошибочно Х% работ и завершающий в срок Y% заданий, не уступает тому, кто выполняет безошибочно 95 % заданий и в срок ___% заданий», мы фактически свернули две переменные в одну.

То же обычно делается с риском и доходностью. С помощью семейства кривых «риск/доходность» мы, взяв эти параметры любых инвестиционных проектов, можем выразить их как доходность, скорректированную на риск. Этот метод свертывания двух разных показателей в один применяют независимо от числа переменных. Если, например, я построил кривые полезности для факторов X и Y, а затем кривые полезности для факторов Y и Z, то каждый сможет построить на их основе кривую полезности для X и Z. Таким путем можно свернуть в единый стандартизированный показатель несколько разнородных факторов, влияющих на такие проблемы, как эффективность деятельности, оценка местоположения нового офиса, выбор линейки новых продуктов и т. п.

Более того, если в одной из комбинаций участвуют деньги, то все остальные факторы можно выразить в деньгах. Когда оценивают инвестиции разной степени рискованности (например, при возможности отрицательной доходности, низкой доходности в случае неблагоприятного развития событий и т. д.) и при этом используют разные показатели доходности (например, внутренняя норма доходности за семь лет, доходность за первый год и т. д.), то иногда полезно объединить все показатели в особый денежный эквивалент (certain monetary equivalent, CME). CME инвестиций — это фиксированная особая сумма в долларах, получить которую инвестор счел бы столь же выгодным, как сделать такое вложение.

Предположим, например, что я хочу приобрести вашу долю в капитале девелоперской компании. За эту долю я предлагаю вам пустующий участок в окрестностях Чикаго стоимостью 200 тыс. дол., с которым вы сможете сделать все, что захотите, или же 100 тыс. дол. наличными немедленно. Будь вам безразлично, какой из вариантов выбрать, стало бы ясно: вы считаете, что CME инвестиций в участок составляет 100 тыс. дол. Если же вы решите, что покупка участка по цене 200 тыс. дол. — очень выгодная сделка, значит, особый денежный эквивалент для этих инвестиций вы оцениваете, скажем, в 300 тыс. дол. Иными словами, вы убеждены, что вариант с покупкой участка выгоден не менее, чем немедленное получение 300 тыс. дол. Можно было строить десятки компромиссных сочетаний, чтобы прийти к такому выводу, но результат остался бы тем же. Сколько бы переменных у вас ни было и какие бы их сочетания ни рассматривались, вы всегда предпочтете 300-тысячный CME сотне тысяч наличными.

Именно так я помогаю многим своим клиентам определить приоритетность инвестиций в информационные технологии, когда существуют разные риски и возможны разные подходы к оценке доходности. Мы сводим все переменные в один CME, определяя желательное соотношение между каждой переменной и неким особым денежным эквивалентом. Это очень мощный инструмент, позволяющий, например, решить, как свернуть в единый денежный показатель 12 разных параметров качества. Хотя ваш выбор и субъективен, вы, тем не менее, получаете количественное представление о компромиссах между разными факторами.

Далее мы рассмотрим ситуации, в которых предпочтительные соотношения между факторами необязательно субъективно определяются лицами, принимающими решения.