Карл Андерсон - Аналитическая культура

Увеличение объема данных может значительно повлиять на показатели из-за простых эффектов. Например, рассмотрим выборку размера n в стандартном нормальном распределении. Как изменяется в зависимости от значения n минимальное значение этой выборки? Создадим выборки разных размеров и вычислим минимальное значение с помощью следующего кода R:

x<-seq(1,7,0.5)

y<-vector(mode="numeric",length=length(x))

for (i in 1:length(x)){ y[i] <- min(rnorm(10^(x[i]))) }

plot(x,y,xlab="Sample size, n (log10 scale)",

ylab="Minimum value of sample",type="b")

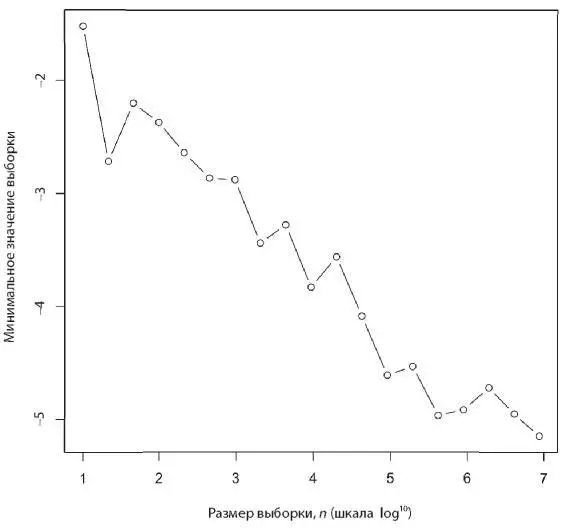
Минимум уменьшается лог-линейно. Это случай экстремума с позиции неограниченного хвоста. Возможно, более подходящей здесь для проблемы минимизации, такой как подбор соответствия, будет нижняя граница — идеальное соответствие для всех целей. Например, возможно, кто-то еще, стоя на том же самом месте, сделал фотографию того же самого вида, но без предмета, портящего фотографию.

Думаю, именно это происходит на графике Норвига. При определенном размере выборки мы нашли очень хорошее соответствие, и увеличение размера выборки уже не может улучшить результат.

Подведем итог: для проблемы минимизации типа «ближайший сосед» с неотрицательной функцией расстояния (что означает, что нижняя граница функции ошибки обучения (cost function) равна нулю) функция расстояния в среднем будет монотонно убывать с размером выборки или данных.

Второй тип — это проблемы относительной частотности . Именно на них сосредоточились Халеви и др. Норвиг приводит несколько примеров. При сегментировании задача заключается в разделении исходного текста, например такого как «cheapdealsandstuff.com», на наиболее вероятные последовательности слов. Эти исходные варианты достаточно короткие, чтобы с ними можно было работать непосредственно с позиции возможного их разделения, но для каждого получившегося отдельного слова нужно оценить вероятность его существования. Самое простое предположение — о независимости среди слов. Таким образом, если Pr ( w ) — это вероятность слова w , то, имея некоторый набор данных, можно вычислить, например:

Pr(che,apdeals,andstuff) = Pr(che). Pr(apdeals). Pr(andstuff).

…

Pr(cheap,deals,and,stuff) = Pr(cheap). Pr(deals). Pr(and).

Pr(stuff).

Конечно, также можно использовать n -граммы (например, биграммы): Pr("cheap deals") × Pr("and stuff").

Второй пример, который привел Норвиг, касался проверки орфографии. В этом случае можно взять слово, содержащее ошибку, и вычислить вероятность возможных вариантов, чтобы предложить наиболее вероятную форму.

В обоих случаях требуется набор данных, содержащий как характерные, так и нехарактерные слова и фразы. Кроме того, необходим показатель встречаемости этих фраз для вычисления относительной частотности. Чем больше и понятнее будет набор данных, тем лучше. Думаю, здесь наблюдаются два статистических явления.

• Чем больше корпус данных, тем выше качество оценки относительной частотности. Это закон больших чисел [280].

• Чем больше корпус данных, тем выше вероятность попадания в него нехарактерных фраз («длинного хвоста»). Это неограниченный эффект. Чем больше индексируется интернет, тем больше новых фраз будет появляться. Проблема осложняется тем, что распределение слов в английском языке — это степенной закон. (См. Zipf, G. The Psycho-Biology of Language. Houghton Mifflin, Boston, MA, 1935.) Это означает наличие особенно длинного хвоста. Следовательно, особенно крупные выборки должны содержать эти редкие фразы.

К третьему типу относятся проблемы оценки одномерного распределения. Недавно я слушал лекцию [281]Питера Скомороха из компании LinkedIn [282]. Он показал распределение вероятности названия должности сотрудника, занимающегося разработкой программного обеспечения, в зависимости от числа месяцев, прошедших после его выпуска из университета. Согласно данным, распределения «Sr Software engineer» и «senior software engineer» (старший инженер-разработчик программного обеспечения) почти идентичны, что можно было ожидать, учитывая их синонимичность. Аналогичная картина и с распределениями «CTO» и «Chief Technology Officer». Это интересный способ определения синонимов и исключения повторов, вместо того чтобы поддерживать длинный основной список акронимов и аббревиатур. Это возможно только благодаря объему данных: при нем распределение, которое делают авторы, — надежное и предположительно близкое к истинному лежащему в основе распределению населения.

Источник: Питер Скоморох. Воспроизводится с разрешения

Четвертый тип проблем — проблемы многофакторности, или корреляционные , при которых мы стремимся оценить взаимоотношения между переменными. Это может быть оценка взаимоотношений y = f(x) или, возможно, оценка совместной плотности распределения многих переменных. Это можно использовать для разрешения лексической многозначности (например, когда в документе встречается слово pike, обозначает ли оно «щуку» или «пику») или для составления «справочника» взаимосвязанных характеристик или концепций для конкретной лексической единицы (например, с понятием «компания» связаны такие понятия, как «генеральный директор», «главный офис», «ИНН» и так далее).

В данном случае нас интересуют корреляции между словами или фразами. Проблема в том, что документы в сети отличаются высокой размерностью, и, принимаясь за решение подобных проблем, мы попадаем под действие «проклятия размерности» [283], когда данные становятся очень рассеянными.

Таким образом, один из эффектов более крупной выборки заключается в повышении плотности данных в статистическом пространстве. Опять-таки, в случае с более крупными выборками есть возможность более точно оценить показатели, такие как показатели положения (среднее значение, медиана и другие показатели центра распределения). Кроме того, можно более точно оценить совместные плотности распределения (PDFs). Следующая диаграмма рассеяния представляет собой простой пример, составленный на основе этого кода:

par(mfrow=c(1,2))

plot(mvrnorm(100, mu = c(0, 0),

Sigma = matrix(c(1, 9, 9, 1), 2)), xlab="X",ylab="Y",

ylim=c(-4,4))

title("n = 100")

plot(mvrnorm(10000, mu = c(0, 0),

Sigma = matrix(c(1, 9, 9, 1), 2)), xlab="X",ylab="Y",

ylim=c(-4,4))

title("n = 10000")

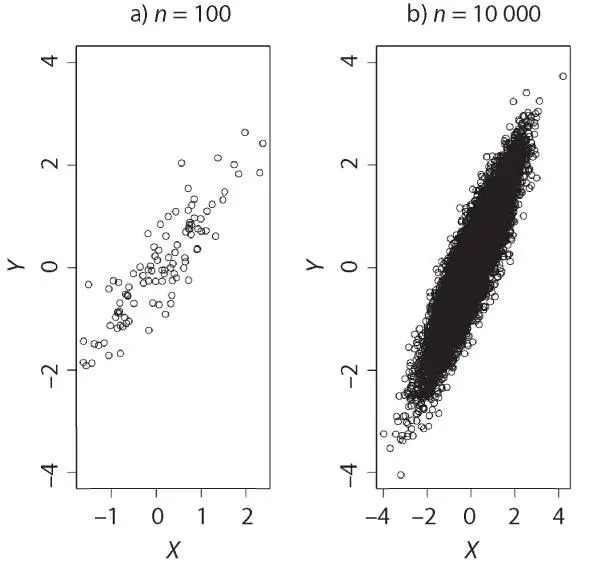
Слева использовалась маленькая выборка. Диаграмму легко интерпретировать как линейную. Справа, где размер выборки был больше, более очевидно настоящее двумерное нормальное распределение. Конечно, это банальный пример. Суть в том, что для более высоких размерностей требуется значительно более серьезный размер выборки, чтобы также оценить совместные плотности распределения.