Чарльз Уилан - Голая статистика

Стандартная ошибка измеряет разброс средних значений выборок. Насколько предположительно близко они будут группироваться вокруг среднего значения совокупности? Здесь возможна некоторая путаница, поскольку вам уже известны два разных показателя разброса: среднеквадратическое (стандартное) отклонение и стандартная (среднеквадратическая) ошибка. Чтобы внести ясность в этот вопрос, нужно учитывать следующее.

1. Среднеквадратическое отклонение измеряет разброс в исходной совокупности. В данном случае оно может измерять разброс значения веса всех участников Framingham Heart Study, то есть разброс вблизи среднего значения для всех зарегистрированных участников марафона.

2. Стандартная ошибка измеряет разброс средних значений выборок . Если мы извлекли ряд выборок (в каждой по 100 значений) из Framingham Heart Study, то как будет выглядеть разброс их средних значений?

3. Вот что связывает между собой эти две концепции: стандартная ошибка является среднеквадратическим отклонением средних значений выборок! Замечательно, не правда ли?

Большая стандартная ошибка означает, что средние значения выборок разбросаны на значительных расстояниях от среднего значения совокупности; малая стандартная ошибка означает, что средние значения выборок располагаются относительно близко вокруг среднего значения совокупности. Ниже приведены три реальных примера на основе данных Americans’ Changing Lives.

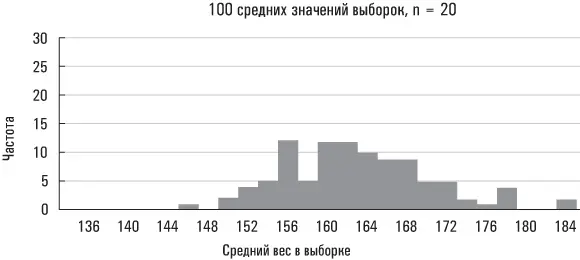
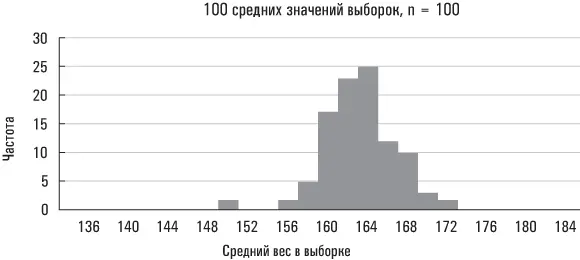
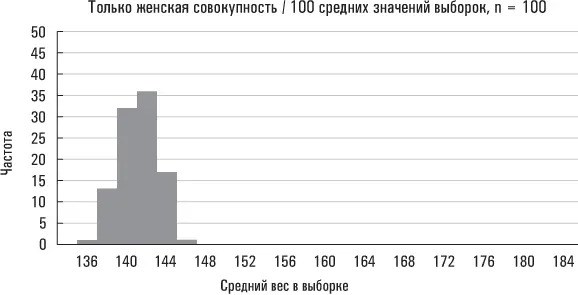
Второе распределение, размер выборки у которого больше, сгруппировано вблизи среднего значения плотнее, чем первое. Больший размер выборки снижает вероятность того, что ее среднее значение существенно отклонится от среднего значения совокупности. Последний набор средних значений выборок получен из подмножества рассматриваемой нами совокупности (в данном случае таким подмножеством являются женщины). Поскольку значения веса женщин в этой совокупности данных разбросаны в меньшей степени, чем значения веса всех лиц в рассматриваемой нами совокупности, вполне естественно, что вес выборок, сформированных исключительно из женской совокупности, должен быть менее разбросанным, чем выборок, извлеченных из всей совокупности Americans’ Changing Lives. (Эти выборки также сгруппированы вблизи несколько отличающегося среднего значения совокупности, так как средний вес всех женщин в исследовании Americans’ Changing Lives разнится со средним весом всей совокупности, охваченной данным экспериментом.)

Нарисованная мной картина носит универсальный характер. Средние значения выборок будут группироваться вблизи среднего значения совокупности более плотно по мере увеличения размера каждой выборки (например средние значения наших выборок группировались вблизи среднего значения совокупности более плотно, когда их размер увеличился с 20 до 100). И менее плотно, когда исходная совокупность окажется более «разбросанной» (например средние значения наших выборок для всей совокупности Americans’ Changing Lives были более разбросанными, чем средние значения выборок лишь для женской совокупности).

Если вам до сих пор удавалось следить за логикой моего изложения, то формула для стандартной ошибки (SE) не потребует дополнительных разъяснений: SE = s ÷ √ n , где s – среднеквадратическое отклонение для совокупности, из которой сформирована данная выборка, а n – размер выборки. Не следует, однако, слишком уповать на формулы. Не забывайте привлекать на помощь интуицию. Стандартная ошибка будет большой, когда среднеквадратическое отклонение исходного распределения велико. Большая выборка, сформированная из сильно разбросанной совокупности, также, скорее всего, окажется сильно разбросанной; большая выборка, сформированная из совокупности, плотно сгруппированной вблизи среднего значения, также, скорее всего, окажется плотно сгруппированной вблизи среднего значения. Если вернуться к примеру с весом, то можно ожидать, что стандартная ошибка для выборки, извлеченной из всей совокупности Americans’ Changing Lives, будет большей, чем стандартная ошибка для выборки, состоящей только из мужчин в возрасте от двадцати до тридцати лет. Именно поэтому среднеквадратическое отклонение (s) находится в числителе приведенной выше формулы .

Аналогично можно ожидать, что стандартная ошибка будет уменьшаться по мере увеличения размера выборки, поскольку большие выборки в меньшей степени подвержены искажению со стороны экстремальных наблюдений («отщепенцев»). Именно поэтому размер выборки n находится в знаменателе формулы. (Разъяснение причины, по которой в формуле используется корень квадратный из n, мы оставим для более «продвинутых» учебников по статистике; в данном случае для нас важны базовые соотношения.)

В случае данных Americans’ Changing Lives нам фактически известно среднеквадратическое отклонение этой совокупности, однако зачастую так не бывает. В отношении крупных выборок мы можем предположить, что их среднеквадратическое отклонение довольно близко к среднеквадратическому отклонению генеральной совокупности [41].

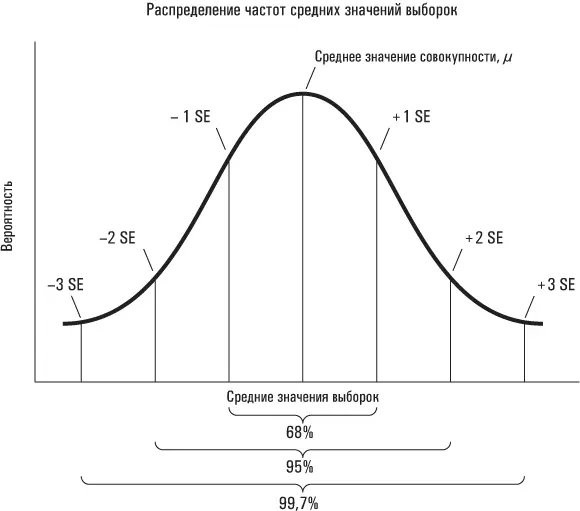
Наконец, настало время подвести итог сказанному. Поскольку средние значения выборок распределены по нормальному закону (благодаря центральной предельной теореме), мы можем воспользоваться богатым потенциалом кривой нормального распределения. Мы рассчитываем, что примерно 68 % средних значений всех выборок будут отстоять от среднего значения совокупности на расстоянии, не превышающем одной стандартной ошибки; 95 % – на расстоянии, не превышающем двух стандартных ошибок; и 99,7 % – на расстоянии, не превышающем трех стандартных ошибок.

Теперь вернемся к отклонению (разбросу) в примере с пропавшим автобусом – правда, на этот раз призовем на помощь не интуицию, а числа. (Сам по себе этот пример остается абсурдным; в следующей главе мы рассмотрим множество более близких к реальности случаев.) Допустим, что организаторы исследования Americans’ Changing Lives пригласили всех его участников на выходные в Бостон, чтобы весело провести время и заодно предоставить кое-какие недостающие данные. Участников распределяют произвольным образом по автобусам и отвозят в тестовый центр, где их взвесят, определят рост и т. п. К ужасу организаторов мероприятия, один из автобусов пропадает где-то по пути в тестовый центр. Об этом событии оповещают в программе новостей местного радио и телевидения. Возвращаясь примерно в то же время в своем автомобиле с Фестиваля любителей сосисок, вы замечаете на обочине дороги сломавшийся автобус. Похоже, его водитель был вынужден резко свернуть в сторону, пытаясь уклониться от столкновения с лосем, неожиданно появившимся на дороге. От столь резкого маневра все пассажиры потеряли сознание или лишились дара речи, хотя никто из них, к счастью, не получил серьезных травм. (Такое предположение понадобилось мне исключительно для чистоты приведенного здесь примера, а надежда на отсутствие у пассажиров серьезных травм объясняется моим врожденным человеколюбием.) Врачи кареты скорой помощи, оперативно прибывшие на место происшествия, сообщили вам, что средний вес 62 пассажиров автобуса составляет 194 фунта. Кроме того, оказалось (к огромному облегчению всех любителей животных), что лось, от столкновения с которым пытался увернуться водитель автобуса, практически не пострадал (если не считать легкого ушиба задней ноги), но от сильного испуга тоже потерял сознание и лежит рядом с автобусом.