Нихиль Будума - Основы глубокого обучения

Прежде чем начать разговор о способах борьбы с переобучением, опишем рабочий процесс создания и обучения моделей глубокого обучения. Он подробно показан на рис. 2.14. Он сложен, но его понимание важно для правильного обучения нейросетей.

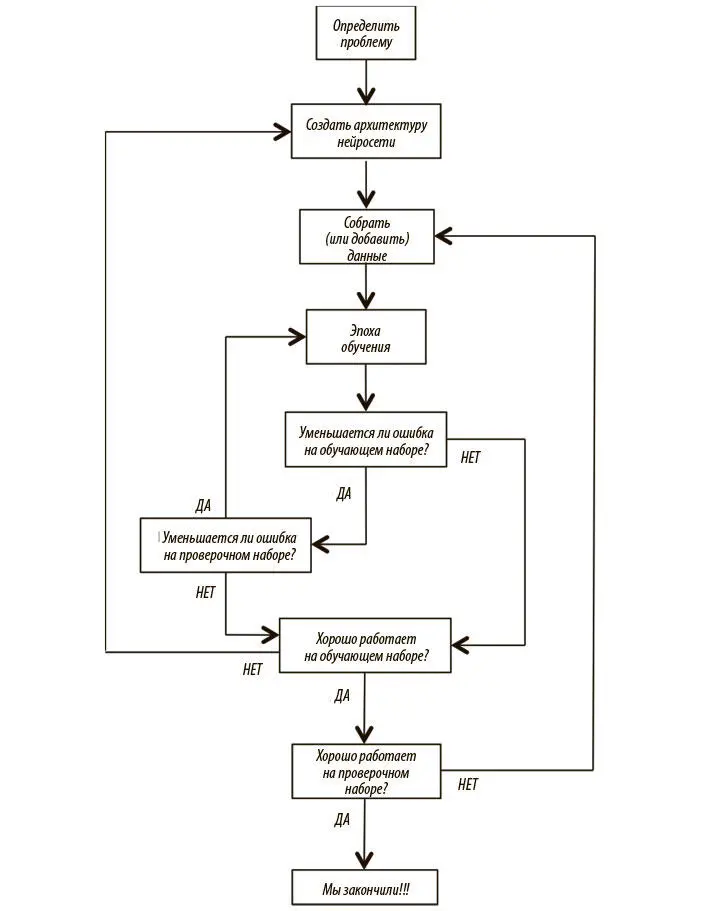
Рис. 2.14. Подробный рабочий процесс и оценки модели глубокого обучения

Сначала необходимо четко определить проблему. Мы рассматриваем входные данные, потенциальные выходные и векторное представление тех и других. Допустим, наша цель — обучение модели для выявления рака. Входные данные поступают в виде изображения в формате RGB, которое может быть представлено как вектор со значениями пикселов. Выходными данными будет распределение вероятностей по трем взаимоисключающим вариантам: 1) норма; 2) доброкачественная опухоль (без метастазов); 3) злокачественная опухоль (рак, давший метастазы в другие органы).

Далее нужно создать архитектуру нейросети для решения проблемы. Входной слой должен иметь достаточные размеры для приема данных изображения, а выходной должен быть размера 3 с мягким максимумом. Нам также следует определить внутреннюю архитектуру сети (количество скрытых слоев, связи и т. д.). В главе 5 мы поговорим об архитектуре моделей для компьютерного зрения, когда будем обсуждать сверточные нейросети. Еще нужно подобрать достаточно данных для обучения или моделирования. Они, возможно, будут представлены в виде фотографий патологий единообразного размера, помеченных медицинским экспертом. Мы перемешиваем эти данные и разбиваем их на обучающий, проверочный и тестовый наборы.

Мы готовы начать градиентный спуск. Мы тренируем модель на обучающем наборе в течение одной эпохи. В конце эпохи мы убеждаемся, что ошибка на обучающем и проверочном наборах уменьшается. Когда улучшения прекращаются, мы останавливаемся и выясняем, устраивают ли нас результаты модели на тестовых данных. Если нет, следует пересмотреть архитектуру или подумать, действительно ли собранные данные содержат информацию, которая требуется для нужного нам предсказания. Если ошибка на обучающем наборе не уменьшается, возможно, стоит поработать над свойствами данных. Если не сокращается ошибка на проверочном наборе, пора принять меры против переобучения.

Если же нас устраивают результаты модели на обучающих данных, мы можем вычислить ее производительность на тестовых данных, с которыми она ранее не была знакома. Если результат неудовлетворителен, требуется добавить данных в обучающий набор, поскольку тестовый, вероятно, содержит примеры, которые были недостаточно представлены в обучающем. Если же все нормально, то мы закончили!

Есть несколько методов борьбы с переобучением. Ниже мы подробно их обсудим. Один из них носит название регуляризации . Он изменяет целевую функцию, которую мы минимизируем, добавляя условия, которые препятствуют появлениям больших весов. Иными словами, мы изменяем целевую функцию на Error + λf( θ ) , где f( θ ) увеличивается, когда компоненты θ растут, а λ — показатель регуляризации (еще один гиперпараметр). Значение λ определяет, в какой степени мы хотим защититься от переобучения. Если λ = 0, мы не принимаем никаких мер. Если λ слишком велико, приоритетом модели будет сохранение θ на низком уровне, а не нахождение значений параметров, которые дадут хорошие результаты на обучающем наборе. Выбор λ — очень важная задача, которая может потребовать ряда проб и ошибок.

Самый распространенный тип регуляризации в машинном обучении — так называемая L2-регуляризация [14]. Ее можно провести, дополнив функцию потерь квадратом величины всех весов в нейросети. Иными словами, для каждого веса w в нейросети мы добавляем 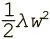в функцию потерь. L2-регуляризация интуитивно интерпретируется как препятствующая появлению пиковых векторов весов и предпочитающая равномерные векторы весов.

Это полезное свойство, побуждающее сеть использовать в равной степени все входные данные, а не отдавать предпочтение одним входам в ущерб другим. К тому же в ходе градиентного спуска использование L2-регуляризации в целом означает, что каждый вес линейно уменьшается до 0. Благодаря этому феномену L2-регуляризация получила второе название: сокращение весов .

Мы можем визуализировать эффекты L2-регуляризации с помощью ConvNetJS. Как на рис. 2.10и рис. 2.11, здесь используется нейросеть с двумя входами, двумя выходами с мягким максимумом и скрытый слой из 20 нейронов. Мы обучаем сети при помощи мини-пакетного градиентного спуска (размер пакета 10) и показателей регуляризации 0,01, 0,1 и 1. Результаты приведены на рис. 2.15.

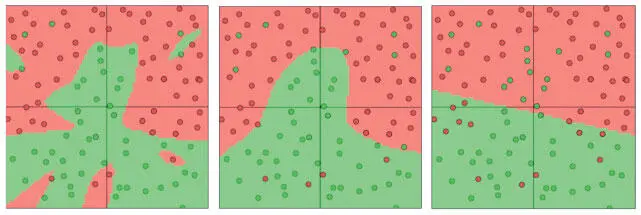
Рис. 2.15. Визуализация нейросетей, обученных с показателями регуляризации 0,01, 0,1 и 1 (в таком порядке)

Еще один распространенный вариант — L1-регуляризация . Здесь мы добавляем значение λ|w| для каждого веса w в нейросети. L1-регуляризация обладает интригующим свойством: в ходе оптимизации векторы весов становятся очень разреженными (очень близкими к 0). Иными словами, нейроны начинают использовать небольшое количество самых важных входов и становятся устойчивыми к шуму на входе. А векторы весов, полученные при L2-регуляризации, обычно равномерны и невелики. L1-регуляризация очень полезна, когда вы хотите понять, какие именно свойства вносят вклад в принятие решения. Если такой уровень анализа свойств не нужен, мы используем L2-регуляризацию: она на практике работает лучше.

Максимальные ограничения нормы имеют схожую цель: это попытка предотвратить слишком большие значения θ, но более непосредственная [15]. Максимальные ограничения нормы задают абсолютную верхнюю границу для входного вектора весов каждого нейрона и при помощи метода проекции градиента устанавливают ограничение. Иными словами, каждый раз, когда шаг градиентного спуска изменяет входящий вектор весов, так что || w || 2 > c, мы проецируем вектор обратно на шар (центр которого расположен в исходной точке) с радиусом c . Типичные значения c — 3 и 4. Примечательно, что вектор параметров не может выйти из-под контроля (даже если нормы обучения слишком высоки), поскольку обновления весов всегда ограничены.

Совсем иной метод борьбы с переобучением — прореживание (Dropout) , который особенно популярен у специалистов по глубоким нейросетям [16]. При обучении он используется так: нейрон становится активным только с некой вероятностью p (гиперпараметр), иначе его значение приравнивается к 0. На интуитивном уровне можно решить, что это заставляет нейросеть оставаться точной даже в условиях недостатка информации. Сеть перестает быть слишком зависимой от отдельного нейрона или их небольшого сочетания. С точки зрения математики прореживание препятствует переобучению, давая возможность приблизительно сочетать экспоненциально большое количество архитектур нейросетей, причем эффективно. Процесс прореживания показан на рис. 2.16.