Анатолий Кондратенко - Вероятностная теория фондовых бирж

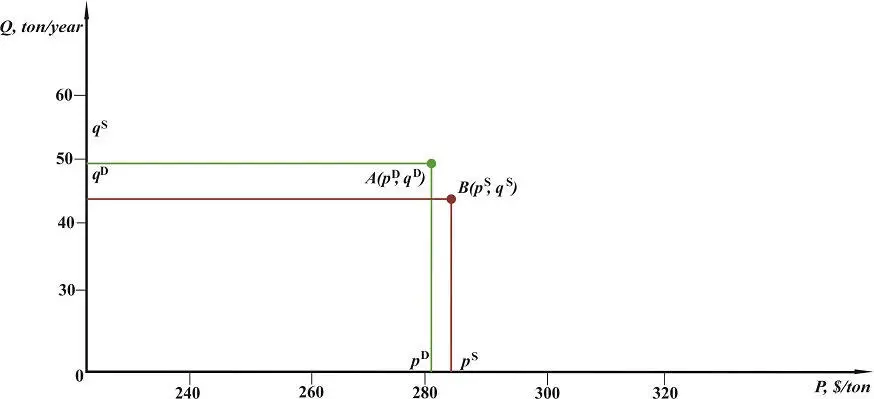
Рис. 1.2. Графическое представление точечной стратегии рыночного поведения покупателя A(p D, q D) и продавца B ( p S, q S) точками в двумерном пространстве цены-количества в некоторый определенный момент времени для модельного рынка зерна. p D= 280,0 $/ ton, q D= 50,0 ton/year, p S= 285,0 $/ ton, q S= 52,0 ton/year.

Мы будем говорить (для краткости) об этом совокупном движении агентов как о поведении рынка, а иногда – как об эволюции экономики во времени. Все эти термины являются, по сути, синонимами в данном контексте обсуждения. Таким образом, выставляя желаемые цены и количества в качестве своих котировок, покупатели и продавцы принимают участие в рыночном процессе, протекающем здесь в формате переговоров между торгующимися людьми (homo negotians), стремящимися выторговать для себя наилучшие условия при заключении сделки и достичь рыночных целей. Заметим, что в действительности в состав действий рыночных агентов наряду с выставлением котировок входят также процедуры заключения итоговых сделок, но последние учитываются в таком подходе автоматически путем изменения заявок рыночными агентами после заключения сделок. Поэтому нет необходимости явным образом включать в состав действий агентов процедуру заключения сделок, достаточно принимать во внимание только процесс выставления ими котировок в течение торгов.

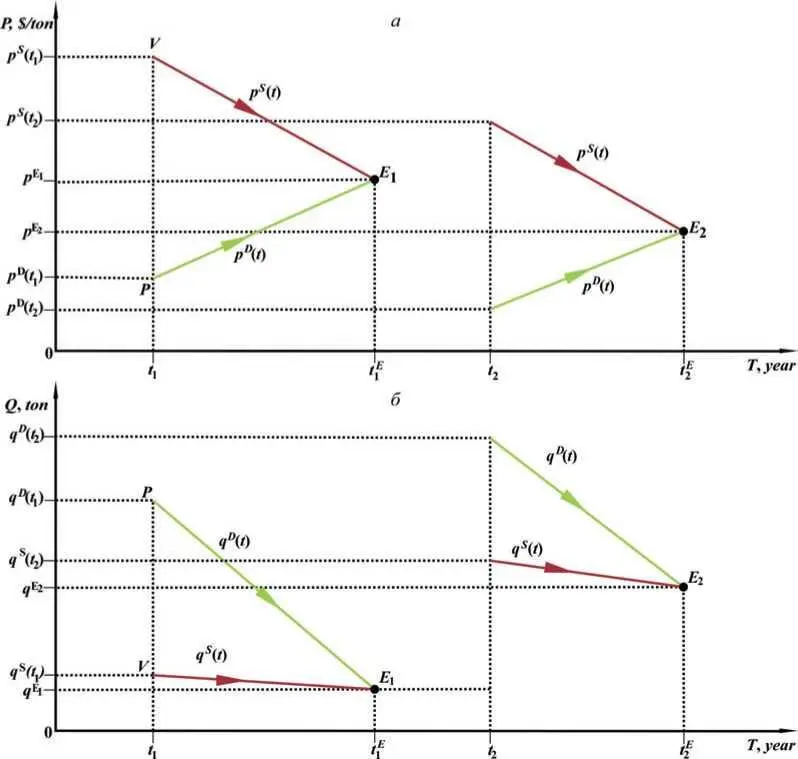
Рис. 1.3. Диаграмма траекторий движения покупателя и продавца. Изображена динамика классической двухагентной рыночной экономики в экономическом пространстве цены (а) и количества (б). В совокупности обе части рисунка представляют эволюцию экономики во времени в двумерном PQ -пространстве.

Можно весь этот торговый процесс, или просто торг, трактовать как динамическую деловую игру между покупателем и продавцом с целью извлечения прибыли или достижения некой другой цели.

Предположим, что переговоры прошли удачно и завершились заключением сделки купли-продажи в момент времени t 1 E . Это означает, что в этот момент времени значения ценовых ( p D ( t ) и p S ( t )), а также количественных ( q D ( t ) и q S ( t )) котировок, становятся равными, так как очевидно, что в контракте могут быть указаны только конкретные взаимно-согласованные цена p 1 E и количество q 1 E товара. Будем полагать, что в этой переговорной модели есть определенный смысл называть данные значения цены и количества рыночными ценой и количеством товара и считать, что сам рынок при этих значениях цены и количества товара приходит в равновесие или достигает своего равновесного состояния. Формально это описывается с помощью следующих равенств для рыночных цены и количества:

Итак, для двухагентной модели мы получили такой тривиальный, но многозначительный результат: сам факт достижения равновесия дает возможность осуществить сделку и максимизировать объем торгов в денежном выражении. Этот вывод в данном простом случае вполне очевиден: нет согласия, нет равновесия, нет сделки, объем торгов нулевой. Но мы покажем далее, что этот вывод имеет достаточно универсальный характер, что согласуется с постулированным принципом максимизации объема торгов. Кстати, легко показать, что в рамках неоклассической теории в точке равновесия достигается максимум объема торгов в натуральном выражении, т.е. достигается максимум количества проданного товара.

Далее, поскольку жизнь не стоит на месте, покупатель и продавец могут еще не раз встречаться и заключать новые сделки, но уже в новых условиях и, очевидно, с другими ценами и количествами, то для удобства мы будем называть p 1 E первой рыночной ценой, а q 1 E – первым рыночным количеством. Таким образом, в момент времени t 1 интересы покупателя и продавца в первый раз совпали, они были оптимальным образом удовлетворены путем заключения сделки купли-продажи. При этом агенты, естественно, в ходе рыночного процесса (переговоров и изменения котировок) неявным образом принимали во внимание влияние внешней окружающей среды и институциональных факторов на этом и других рынках, т.е. экономики в целом. Здесь можно заметить схожесть в движении экономической системы в экономическом пространстве, описываемом с помощью траекторий покупателя p D ( t ) и q D ( t ) и продавца p S ( t ) и q S ( t ), и в движении двухчастичной физической системы в реальном пространстве, описываемом траекториями частиц х 1 ( t ) и х 2 ( t ), которые, кстати, также являются результатом действия определенного физического принципа максимизации, а именно принципа наименьшего действия на физическую систему.

Отмеченная аналогия с физической системой наводит на мысль использовать аналогичный математический аппарат, аналитический и графический. На рис. 1.3, для начала, мы даем графическое представление этих траекторий движения агентов в зависимости от времени с помощью подходящих систем координат время – цена ( T, P ) и время – количество ( T, Q ), аналогично тому, как происходит построение траекторий частиц в классической механике. Заметим, что рис. 1.3 отражает определенную стандартную ситуацию на рынке, когда покупатель и продавец намеренно встречаются в момент времени t 1 и начинают обсуждать потенциальную сделку путем взаимного обмена информацией об их условиях, прежде всего желаемых цен и количества товара. Во время переговоров они непрерывно изменяют свои котировки до тех пор, пока не соглашаются на окончательные условия по цене p 1 E и количеству q 1 E в момент времени t 1 E . Такая простейшая «переговорная» рыночная модель применима, например, для экономики вымышленного острова, на котором, скажем для определенности, раз в году путем переговоров происходит торговля зерном между фермером и охотником. Для определенности, будем считать, что они используют для расчетов американский доллар, $. Для наглядности, на рис. 1.3, как и на последующих рисунках, мы используем стрелки для отражения направления движения агентов во время рыночного процесса.

Итак, в нашей переговорной классической модели вплоть до момента t 1 рынок находится в простейшем состоянии покоя, здесь нет торговли вообще. В момент времени t 1 на рынке появляются покупатель и продавец зерна, которые устанавливают свои начальные желаемые цены и количество зерна: p D ( t 1 ), p S ( t 1 ) и q D ( t 1 ), q S ( t 1 ). Точки P и V на графике показывают положение покупателя и продавца в начальный момент времени t 1 , когда начинаются торговые переговоры. Естественно, желания покупателя и продавца сразу не совпадают, покупатель хочет низкую цену, но продавец борется за более высокую цену. Однако оба нуждаются в достижении понимания и последующего заключения сделки, в противном случае фермер и охотник будут иметь трудный следующий год. Переговорный процесс продолжается, рыночный процесс изменения агентами их котировок отражает его ход. Как результат, позиции рыночных агентов сходятся, и они совпадают в момент времени t 1 E , который соответствует точке пересечения траекторий E 1на графиках.