Инесса Бурханова - Теория статистики: конспект лекций

Средняя величина абстрактна, так как характеризует значение абстрактной единицы.

От разнообразия признака у отдельных объектов абстрагируется средняя. Абстракция – ступень научного исследования. В средней величине осуществляется диалектическое единство отдельного и общего.

Средние величины должны применяться исходя из диалектического понимания категорий индивидуального и общего, единичного и массового.

Средняя отображает что–то общее, которое складывается в определенном единичном объекте.

Для выявления закономерностей в массовых общественных процессах средняя величина имеет большое значение.

Отклонение индивидуального от общего – проявление процесса развития.

В средней величине отражается характерный, типичный, реальный уровень изучаемых явлений. Задачей средних величин является характеристика этих уровней и их изменений во времени и пространстве.

Средний показатель – это обычное значение, потому что формируется в нормальных, естественных, общих условиях существования конкретного массового явления, рассматриваемого в целом.

Объективное свойство статистического процесса или явления отражает средняя величина.

Индивидуальные значения исследуемого статистического признака у каждой единицы совокупности различны. Средняя величина индивидуальных значений одного вида – продукт необходимости, который является результатом совокупного действия всех единиц совокупности, проявляющийся в массе повторяющихся случайностей.

Одни индивидуальные явления имеют признаки, которые существуют во всех явлениях, но в разных количествах – это рост или возраст человека. Другие признаки индивидуального явления, качественно различные в различных явлениях, т. е. имеются у одних и не наблюдаются у других (мужчина не станет женщиной). Средняя величина вычисляется для признаков качественно однородных и различных только количественно, которые присущи всем явлениям в данной совокупности.

Средняя величина является отражением значений изучаемого признака и измеряется в той же размерности, что и этот признак.

Теория диалектического материализма учит, что все в мире меняется, развивается. А также изменяются признаки, которые характеризуются средними величинами, а соответственно – и сами средние.

В жизни происходит непрерывный процесс создания чего–то нового. Носителем нового качества являются единичные объекты, далее количество этих объектов возрастает, и новое становится массовым, типичным.

Средняя величина характеризует изучаемую совокупность только по одному признаку. Для полного и всестороннего представления изучаемой совокупности по ряду определенных признаков необходимо располагать системой средних величин, которые могут описать явление с разных сторон.

В статистической обработке материала возникают различные задачи, которые необходимо решать, и поэтому в статистической практике используются различные средние величины. Математическая статистика использует различные средние, такие как: средняя арифметическая; средняя геометрическая; средняя гармоническая; средняя квадратическая.

Для того чтобы применить одну из вышеперечисленных видов средней, необходимо проанализировать изучаемую совокупность, определить материальное содержание изучаемого явления, все это делается на основе выводов, полученных из принципа осмысленности результатов при взвешивании или суммировании.

В изучении средних величин применяются следующие показатели и обозначения.

Признак, по которому находится средняя, называется осредняемым признаком и обозначается х; величина осредняемого признака у любой единицы статистической совокупности называют индивидуальным его значением,или вариантами,и обозначают как x 1 , х 2 , x 3 ,… х п ; частота – это повторяемость индивидуальных значений признака, обозначается буквой f.

Средняя арифметическая

Один из наиболее распространенных видов средней – средняя арифметическая, которая исчисляется тогда, когда объем ос–редняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности.

Для вычисления средней арифметической величины сумму всех уровней признака делят на их число.

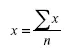
Если некоторые варианты встречаются несколько раз, то сумму уровней признака можно получить умножением каждого уровня на соответствующее число единиц совокупности с последующим сложением полученных произведений, исчисленная таким образом средняя арифметическая называется средней арифметической взвешенной.

Формула средней арифметической взвешенной выглядит следующим образом:

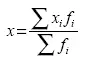
гдех i– варианты,

f i– частоты или веса.

Взвешенная средняя величина должна употребляться во всех случаях, когда варианты имеют различную численность.

Арифметическая средняя как бы распределяет поровну между отдельными объектами общую величину признака, в действительности варьирующуюся у каждого из них.

Вычисление средних величин производят по данным, сгруппированным в виде интервальных рядов распределения, когда варианты признака, из которых исчисляется средняя, представлены в виде интервалов (от – до).

Свойства средней арифметической:

1) средняя арифметическая суммы варьирующих величин равна сумме средних арифметических величин: Если х i= y i+z i, то

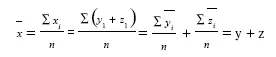
Данное свойство показывает в каких случаях можно суммировать средние величины.

2) алгебраическая сумма отклонений индивидуальных значений варьирующего признака от средней равна нулю, так как сумма отклонений в одну сторону погашается суммой отклонений в другую сторону:

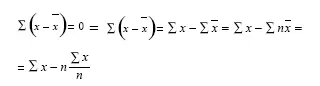
Это правило демонстрирует, что средняя является равнодействующей.

3) если все варианты ряда увеличить или уменьшить на одно и тоже число α, то средняя увеличится или уменьшится на это же число α:

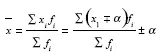
4) если все варианты ряда увеличить или уменьшить в А раз, то средняя также увеличится или уменьшится в А раз:

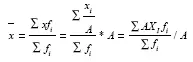
5) пятое свойство средней показывает нам, что она не зависит от размеров весов, но зависит от соотношения между ними. В качестве весов могут быть взяты не только относительные, но и абсолютные величины.