Инесса Бурханова - Теория статистики: конспект лекций
- Название:Теория статистики: конспект лекций
- Автор:
- Жанр:
- Издательство:Конспекты, шпаргалки, учебники «ЭКСМО»b4455b31-6e46-102c-b0cc-edc40df1930e
- Год:2007
- Город:Москва
- ISBN:978-5-699-24123-1
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Инесса Бурханова - Теория статистики: конспект лекций краткое содержание
Данное учебное пособие предназначено для подготовки студентов экономических вузов к сдаче экзаменов. Издание содержит полный курс лекций по теории статистики, составленный профессиональными экономистами. Студентам предлагается ознакомиться с вопросами теории статистики. Рассматриваются методы статистического наблюдения, сводка, групировка данных, средней величины, показатели вариации, корреляционный и регрессивный анализы, анализ временных рядов, индексы, использование графического метода и многое другое.
Издание предназначено для студентов, обучающихся по специальности «Статистика» и другим экономическим специальностям.
Теория статистики: конспект лекций - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Если все частоты ряда разделить или умножить на одно и тоже число d, то средняя не изменится.
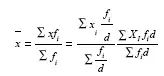
Средняя гармоническая.Для того чтобы определить среднюю арифметическую, необходимо иметь ряд вариантов и частот, т. е. значения х и f.
Допустим, известны индивидуальные значения признака х и произведения х/, а частоты f неизвестны, тогда, чтобы рассчитать среднюю, обозначим произведение = х/; откуда:
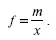
Далее преобразуем формулу средней арифметической так, чтобы по существующим данным хи m исчислить среднюю. Выразив в формуле средней арифметической / через х и m, получим:
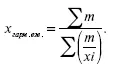
Средняя в этой форме называется средней гармонической взвешенной и обозначается х гарм. взв.
Соответственно, средняя гармоническая тождественна средней арифметической. Она применима, когда неизвестны действительные веса f , а известно произведение fх = z
Когда произведения fх одинаковы или равны единицы (m = 1) применяется средняя гармоническая простая, вычисляемая по формуле:
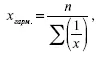
где х – отдельные варианты;
n – число.
Средняя геометрическая
Если имеется n коэффициентов роста, то формула среднего коэффициента:
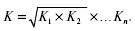
Это формула средней геометрической.
Средняя геометрическая равна корню степени n из произведения коэффициентов роста, характеризующих отношение величины каждого последующего периода к величине предыдущего.
Если осреднению подлежат величины, выраженные в виде квадратных функций, применяется средняя квадратическая. Например, с помощью средней квадратической можно определить диаметры труб, колес и т. д.
Средняя квадратическая простая определяется путем извлечения квадратного корня из частного от деления суммы квадратов отдельных значений признака на их число.
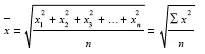
Средняя квадратическая взвешенная равна:
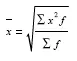
3. Структурные средние величины. Мода и медиана
Для характеристики структуры статистической совокупности применяются показатели, которые называют структурными средними.К ним относятся мода и медиана.
Мода (М о )– чаще всего встречающийся вариант. Модойназывается значение признака, которое соответствует максимальной точке теоретической кривой распределений.
Мода представляет наиболее часто встречающееся или типичное значение.
Мода применяется в коммерческой практике для изучения покупательского спроса и регистрации цен.
В дискретном ряду мода – это варианта с наибольшей частотой. В интервальном вариационном ряду модой считают центральный вариант интервала, который имеет наибольшую частоту (частность).
В пределах интервала надо найти то значение признака, которое является модой.
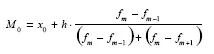
где х о – нижняя граница модального интервала;
h – величина модального интервала;
f m – частота модального интервала;
f т —1– частота интервала, предшествующего модальному;
f m +1– частота интервала, следующего за модальным.
Мода зависит от величины групп, от точного положения границ групп.
Мода– число, которое в действительности встречается чаще всего (является величиной определенной), в практике имеет самое широкое применение (наиболее часто встречающийся тип покупателя).
Медиана (M e – это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения варьирующего признака меньшие, чем средний вариант, а другая – большие.
Медиана– это элемент, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения.
Свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины.
Применение медианы позволяет получить более точные результаты, чем при использовании других форм средних.
Порядок нахождения медианы в интервальном вариационном ряду следующий: располагаем индивидуальные значения признака по ранжиру; определяем для данного ранжированного ряда накопленные частоты; по данным о накопленных частотах находим медианный интервал:
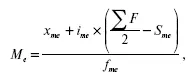
где х ме – нижняя граница медианного интервала;
i Me – величина медианного интервала;
f/2 – полусумма частот ряда;
S Me —1– сумма накопленных частот, предшествующих медианному интервалу;
f Me – частота медианного интервала.
Медиана делит численность ряда пополам, следовательно, она там, где накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая (накопленная) частота меньше половины численности совокупности.
ЛЕКЦИЯ № 8. Показатели вариации
1. Понятие вариации
Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака.Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов (условий), которые по–разному сочетаются в каждом отдельном случае.
Колебания отдельных значений характеризуют показатели вариации.
Термин «вариация» произошел от лат. variatio – «изменение, колеблемость, различие». Под вариациейпонимают количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают вариацию признака: случайную и систематическую.
Систематическая вариация помогает оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов.
Абсолютные и средние показатели вариации и способы их расчета
Для характеристики колеблемости признака используется ряд показателей, такие как размах вариации, определяемый как разность между наибольшим (х мах) и наименьшим (х тщ) значениями вариантов:
Читать дальшеИнтервал:
Закладка:










