Джей Форрестер - Основы кибернетики предприятия

Наконец, встает вопрос об объеме фирмы, для которой динамическое моделирование более всего подходит. По первой общей предпосылке оно является орудием для использования главным образом в крупнейших предприятиях. Так как этот метод сильно развился, для такого вывода других оснований, как будто, не требуется. В больших организациях функциональные перегородки обычно бывают сильнее, чем в небольших фирмах, затрудняя этим прохождение человека через все виды деятельности — от исследования до сбыта. Начинает казаться, что ввиду быстрого роста организации среднего и малого объема могут стать тем местом, где рассмотренные в этой книге методы могут получить вначале наиболее удачное применение. Такие организации часто более гибки. Они могут быть более отзывчивыми на. предложения служащих фирмы, так что при желании последних исследовать новый метод управления такие организации идут им скорее навстречу. В более новых фирмах руководство часто моложе, надеется удержаться на службе дольше и принимает более долгосрочный план развития компании, чем это делается в более старых фирмах. Расходы на исследования систем управления невелики, и они не вызывают трудностей в организации с годовой продукцией в 1 млн. долл.

Ввиду организационного риска и неуверенности в подборе подходящего квалифицированного человека нет также уверенности в первоначальном успехе любой программы динамического моделирования. Однако такой же риск имеется во многих других случаях, где потенциальные выгоды не так велики. Здесь идет игра на ставки, сравнимые с обычной ожидаемой предельной прибылью в промышленности.

В разделе 6.5 рассмотрены правила выбора интервала DT при решении уравнений модели динамической системы. Следовало бы вновь прочесть этот раздел, прежде чем переходить к настоящему приложению.

Выбор интервала зависит от взаимоотношений уровней и темпов потоков в системе. Уровни взаимосвязаны с входящими и исходящими потоками через среднюю величину запаздывания, которое они испытывают в данном уровне. Такое суждение правильно в отношении всех уровней, а не только тех, которые проявляются в формах, называемых нами запаздываниями. Когда интервал решения становится слишком большим, содержимое уровня может оказаться сравнимым с тем количеством, которое поступает или исходит из уровня в течение данного интервала времени. Если это случается, то либо интервал решения слишком продолжителен, либо уровень, о котором идет речь, потерял свое значение в системе и может быть опущен из рассмотрения (почтовые запаздывания не учитывались при рассмотрении модели производственно-сбытовой системы в главе 13).

Влияние изменения интервала решения можно проследить, рассмотрев уравнения запаздываний первого порядка (см. главу 8, уравнения 8–1 и 8–2).

LEV.K = LEV.J+(DT)(IN.JK-OUT.JK)

.

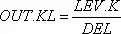Предположим, что запаздывание вначале отсутствует; при этом темпы входящего и исходящего потоков равны нулю; скачок темпа входящего потока в одну единицу за единицу времени имеет место в момент времени, равный нулю. На рис. A-1 показаны итоговые кривые при различных отношениях величины интервала решения ко времени запаздывания, DT/DEL. По горизонтальной оси отложена отвлеченная величина отношения времени к величине запаздывания DEL.

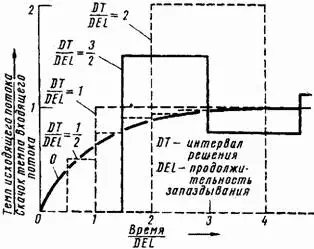
Если интервал решения пренебрежимо мал, то практически в результате получается экспоненциальная кривая, показанная на графике для интервала, равного 0. Когда DT составляет половину от DEL, то в первой расчетной точке уровень, как и величина выходного темпа, достигает половины своего конечного значения. Остающаяся разница между выходными и входными темпами сокращается за каждый интервал времени наполовину.

Если интервал решения равен времени запаздывания, то уровень и темп исходящего потока достигают своих конечных величин к моменту окончания первого этапа вычислений. Экспоненциальное запаздывание приобретает некоторые черты, характерные для запаздывания в каналах снабжения. (Однако таким способом нельзя определять общее запаздывание в каналах снабжения.)

Для еще больших интервалов решений первый вычисленный уровень (как для кривой при DT= 3/ 2времени запаздывания) превысит его установившуюся величину. Темп выхода превысит темп входа. На следующем этапе вычислений величина уровня получится меньше своего установившегося значения. Если интервал решения находится между DEL и 2 (DEL), то в кривой выхода возникнут затухающие колебания.

При DT, равном 2 (DEL), при появлении скачка на входе на выходе возникнут незатухающие колебания. Если интервал решения DT больше, чем 2 (DEL), то колебания на выходе величины будут непрерывно возрастающими.

Кривая на рис. А-1 для интервала решения, равного половине постоянной запаздывания, вероятно, является приемлемым приближением, если только некоторые из запаздываний в системе приблизятся к выбранному значению интервала решения.

Следует иметь в виду, что запаздывание третьего порядка состоит из трех запаздываний первого порядка. Если для каждого из них принимать отношение DTIDEL — 1/ 2, то интервал решения в этом случае должен быть равен или меньше 1/ 6от постоянной времени запаздывания любого экспоненциального запаздывания третьего порядка.

Критерий, использованный здесь для выбора интервала решения, обусловлен структурой системы и ее внутренними динамическими свойствами. Выбор величины интервала между вычислениями в модели нельзя связывать с таким фактором, как периодичность, с которой возможен сбор информации в моделируемой реальной системе. Интервалы решения, выбранные по предложенной здесь методике, будут гораздо короче тех, которые упоминались в литературе по экономическим моделям, и иногда составляли год, даже тогда, когда изучались кратковременные ежегодные изменения в системе.

Влияние величины интервала решения может быть определено эмпирически, с помощью ряда проигрываний модели с тем, чтобы выяснить, в какой мере величина интервала решения сказывается на результатах. Это было сделано на модели (рис. 15-9) фирмы, выпускающей детали электронного оборудования с учетом ранее применявшихся методов управления при величине TBLAF, равной 40 неделям. Результаты приведены на рис. A-2.