Джей Форрестер - Основы кибернетики предприятия

DT — интервал решения (единицы времени);

Т — постоянная времени экспоненциального выравнивания (единицы времени);

S — переменная величина, которая подвергается выравниванию (в соответствующих единицах измерения).

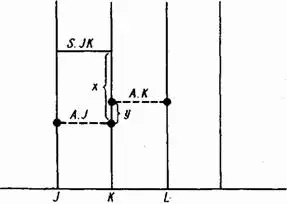
Схематически экспоненциальное выравнивание показано на рис. B–1. В начале вычислений, в момент времени К, известно старое значение средней величины A.J. Выравниваемая величина обозначена S.JK. Разность (S.JK — A.J ), входящая в уравнение В-1 и обозначенная х, будучи умноженной на 1/ T, дает необходимую коррекцию для каждой целой единицы времени; умножая затем эту величину на DT, мы определим коррекцию на данном интервале решения у.

Теперь мы остановимся на рассмотрении запаздываний в потоках информации, которые возникают в результате ее усреднения. Сопоставим уравнение В-1 с обычной парой уравнений, используемых для отображения экспоненциального запаздывания первого порядка.

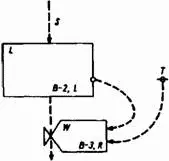
Допустим, что S в уравнении В-1 является вводом в запаздывание, выход из которого обозначен индексом W (см. рис. B–2). Уравнения экспоненциального запаздывания первого порядка могут быть представлены в следующем виде:

,

,

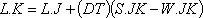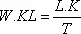где

L — уровень в запаздывании (единицы S, умноженные на время);

S — входящий поток информации (в своих единицах измерения);

W — исходящий поток из запаздывания (те же единицы, что и S );

Т — постоянная времени экспоненциального выравнивания (единицы времени).

Уравнение В-3 может быть записано для более раннего периода:

.

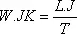Подставив это значение в уравнение В-2, получим

.

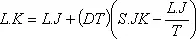Если мы теперь предположим, что L.K = (T)(A.K) , то после простых преобразований получим уравнение

,

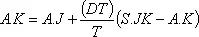которое идентично уравнению В-1. Следовательно, уравнение экспоненциального выравнивания и уравнение запаздывания первого порядка эквивалентны.

Экспоненциальное выравнивание первого порядка вызывает запаздывание в потоках информации той же величины и формы, что и экспоненциальное запаздывание первого порядка. Постоянная времени выравнивания эквивалентна постоянной запаздывания, которая рассматривалась в главе 8.

Запаздывание, создаваемое выравниванием, может быть представлено графически. На рис. В-3 представлено равномерное усреднение.

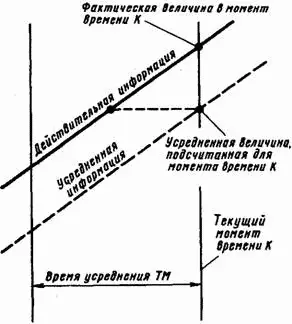
Действительные значения рассматриваемой переменной показаны равномерно увеличивающимися. В любой момент времени средняя величина равна значению действительной величины в середине периода усреднения; другими словами, средняя величина равна действительной с запаздыванием в 1/ 2интервала усреднения.

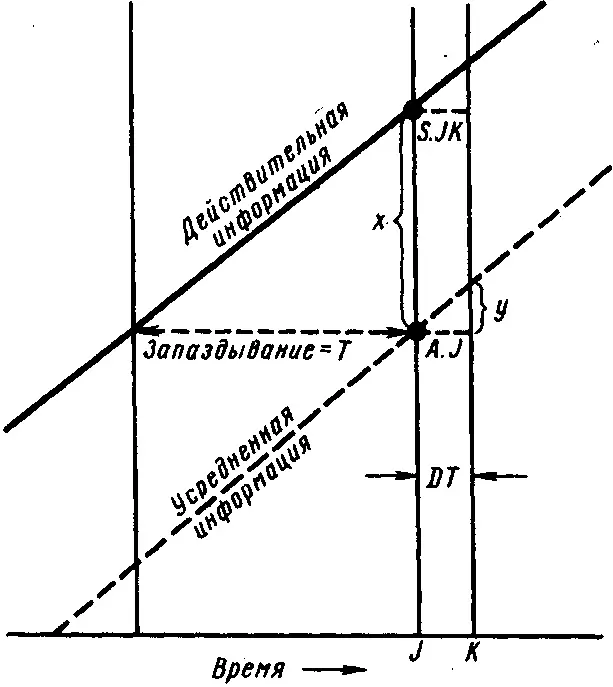
На рис. В-4 показано запаздывание при экспоненциальном выравнивании для случая равномерно возрастающей переменной. Как видно из графиков, запаздывание должно быть равным постоянной времени T ; это можно легко доказать, рассмотрев подобные треугольники:

,

,

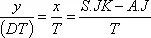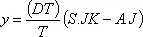где у является изменением среднего значения величины, изображенной на рисунке, и равно правой части уравнения B–1, которое так же отражает изменение значения средней величины. Поэтому величина Т, отображающая на рисунке запаздывание в получении среднего значения по сравнению с действительным, обязательно должна быть равна по величине постоянной времени в уравнении B–1.

Постоянное запаздывание, обусловленное экспоненциальным выравниванием, как это показано на рис. В-4, имеет место только в случае линейно изменяющихся входных данных. При нелинейных потоках информации запаздывание, связанное с выравниванием, будет определяться более сложно. Можно показать, что для синусоидально изменяющихся входных данных запаздывание никогда не превышает четверти периода колебания на входе.

При выравнивании поток информации искажается как по амплитуде, так и во времени. Характер искажений зависит от величины изменений, которые вносятся во входную информацию, от используемого типа выравнивания и объема выравнивания, который определяется видом и степенью нежелательных возмущений, существующих в информации. Почти все потоки информации выравниваются либо посредством формальных математических приемов, либо под воздействием психологических суждений, либо с использованием того и другого методов выравнивания, прежде чем они лягут в основу принимаемых решений. Запаздывания и усиления, обусловленные процессом выравнивания, как мы видели в части III, существенно влияют на динамическое поведение системы.

Даже в тех случаях, когда модель проигрывается при отсутствии помех (как это изображено на большинстве рисунков в части III), процессы выравнивания должны быть отражены в модели. Выравнивание, обусловленное присутствием помех, неизбежно проявляется как фильтр, искажающий желаемую информацию. Эти искажения должны быть отражены даже при отсутствии помех, если мы хотим, чтобы система была правильно отображена в модели.

При работе с моделями замкнутых информационных систем необходимо четко понимать природу и происхождение шумов. Функции принятия решений, которые мы можем сформулировать, объясняют только главные факторы, влияющие на основные потоки. Многочисленные явления возникают за пределами изучаемой системы. Как отмечалось ранее в приложении В, наличие шумов, то есть случайных явлений, требует выравнивания, сглаживания данных, что в свою очередь вызывает запаздывания. Как видно из рис. 13–20 и 15-5, шумы порождают такие возмущения, к которым система чувствительна. Специальное исследование показывает, что шумы ограничивают возможность прогнозирования будущего состояния системы.