Владислав Масликов - Универсум. Общая теория управления

Следует также отметить, что традиционный подход обходит молчанием вопрос возможных отклонений траектории движения системы в случае отсутствия внешнего воздействия (наличия предельно ровной поверхности «тарелки»), ограничивая ответ некоторыми случайным и несущественными «девиациями».

Очевидно, что различные схемы управления для одних и тех же объектов в одних и тех же условиях обеспечивают как различную гибкость реагирования на возмущающие воздействия, так и различный максимально достижимый уровень устойчивости и качества управления.

Более полное раскрытие термина «устойчивость управления» требует рассмотрения различных траекторий достижения системами целевой функции в связи с их фазовыми характеристиками. Вопрос устойчивости процесса управления тесно связан с алгоритмикой работы схем, по которым оно осуществляется, с соотношением фазовых величин ОС восходящего и ПС нисходящего U-потока, образующих внутренние интегративные U-потоки положительной обратной связи (ПОС) и отрицательной обратной связи (ООС). В модели и терминологии импульсных и колебательных процессов этим связям будут соответствовать определённые траектории поведения системы.

Работа программной схемы (рис. 6.10а), реагируя на строго определённые входные состояния системы S, «вмешивается» в процесс управления преимущественно однозначным, дискретным способом. На траектории поведения системы чаще всего это может отражаться как «точка перелома». После осуществления программной реакции R система переходит в режим ожидания очередного однозначно определённого состояния S для выдачи соответствующей ему реакции R. Реакция на состояния системы, не предусмотренные программой, не осуществляется, балансный режим выполняется только в узких рамках набора запрограммированных SR-пар типа «Известный стимул – Соответствующая реакция» (УФУ-1).

Работа адаптивной схемы (рис. 6.10б) в классическом варианте описания поведения объекта при внешнем воздействии на него может быть представлена в виде некоторого отклонения от процесса идеального поведения с последующим возвращением на траекторию, близкую к идеальному режиму управления. Колебательный процесс траектории поведения объекта вокруг заданной траектории соответствует поведению шара в тарелке. Именно этот процесс классической теории управления признаётся критерием устойчивого поведения систем «по Ляпунову» (УФУ-3). Адаптивная схема реагирует на внешние воздействия с небольшим фазовым запаздыванием, она охвачена менее глубокой ООС.

Работа «межеумочной» (нулевой) схемы (рис. 6.10в) соответствует примерному равенству фаз ОС и ПС и, следовательно примерно нулевым значениям ООС и ПОС, что может привести систему в неустойчивый режим со случайными девиациями траектории поведения.

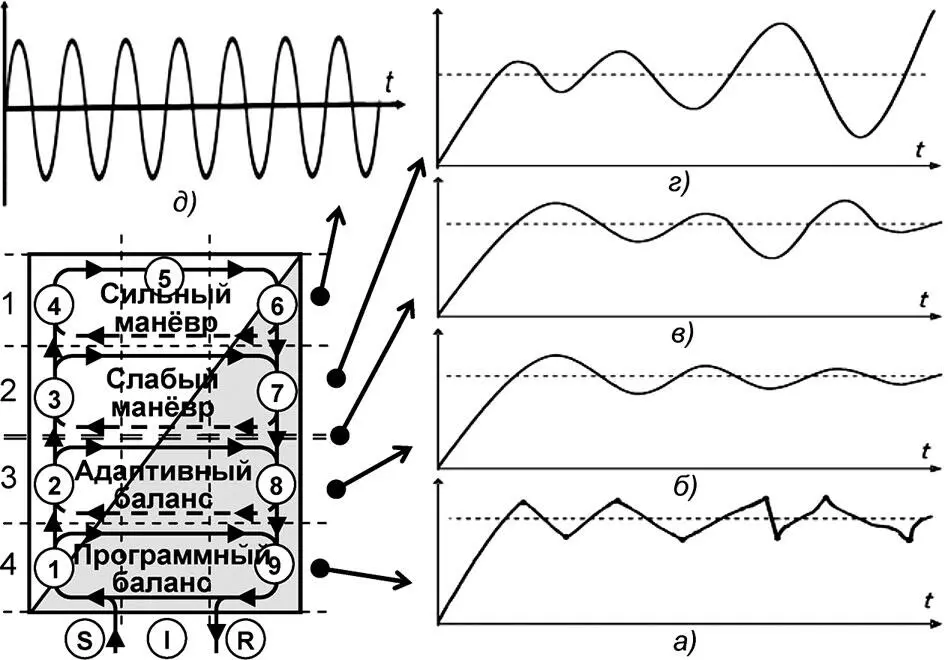
Рис. 6.10. Соответствие U-стратификации режимам управления и траекториям колебательных процессов

Работа предикционной схемы (рис. 6.10 г), осуществляющей слабый манёвр, соответствует неустойчивому варианту поведения шара в тарелке классической теории управления. С универсумной же точки зрения именно возможность «амплитудной раскачки» процесса управления позволяет системе подобрать новый, необходимый для «выживания» адаптационный вариант реакции на внешние воздействия (УФУ-5).

Работа прогностической (интеллектуальной) схемы (рис. 6.10д в электронной аналогии соответствует режиму U-потока OC с большим опережением фазой ПС, что соответствует сильной ПОС, способной перевести систему в режим автогенерации и/или близкий к автогенерации колебаний. Эта схема обладает максимальной устойчивостью, поскольку в максимально полной мере способна обеспечить вероятностную предсказуемость траектории поведения системы. Расчёт параметров «точки будущего» траектории системы, находящейся в состоянии автогенерации не представляет затруднений.

Траекторное описание термина «устойчивость» позволяет сделать ряд выводов, связанных с тем, что восходящий U-поток ОС имеет источником стимулы S, воздействующие на систему, а U-поток ПС определяет реакцию R системы на эти воздействия (рис. 6.11).

В универсумном описании программная и адаптивная схемы управления системой соответствуют балансировочному режиму работы.

Балансировочный режим – это ситуация, когда описывающий траекторию движения системы вектор состояния колеблется относительно неизменного положения в подпространстве контрольных параметров. Это тактика решения задач, реализуемая в рамках определённой стратегии посредством адаптационного и программного режимов работы. Программный режим обеспечивает решение стандартных оперативных действий, принимаемых в рамках конкретных тактических задач. Он также может использоваться и на «надёжных» участках траекторий, на которых объект достаточно хорошо застрахован от нежелательных внешних воздействий [167]. Для работы системы в балансировочном режиме достаточно одного комплекта векторов управления (целей, состояния и ошибки управления), значения которых изменяются в определённых, достаточно небольших пределах. Выход траектории (вектора ошибки) за пределы допустимых величин требует от системы способности осуществления слабого манёвра.

Для проведения манёвров, представляющих предикционную и интеллектуальную схемы управления, необходимо уже не менее двух комплектов, отличающихся друг от друга ранжированием и/или набором целей векторов управления.

Рассмотрим устойчивость этих схем более подробно с точки зрения фазовых характеристик U-потоков различных типов связей.

1) Программная схема управления (контур 1–9 максимально сдвинутой «в прошлое» фазы ООС), не используя в качестве обратной связи динамические параметры внешней среды, максимально устойчива по запрограммированным для отработки воздействиям. Как максимально глубокая ООС она работает по жёстко заданной программе, конструктивно-механически. Реализацию накопленного в прошлом опыта может представлять, например, форма корпуса, стабилизирующая объект (корабль, самолёт) на заданном курсе или в заданном пространстве параметров даже без непосредственного управляющего воздействия.

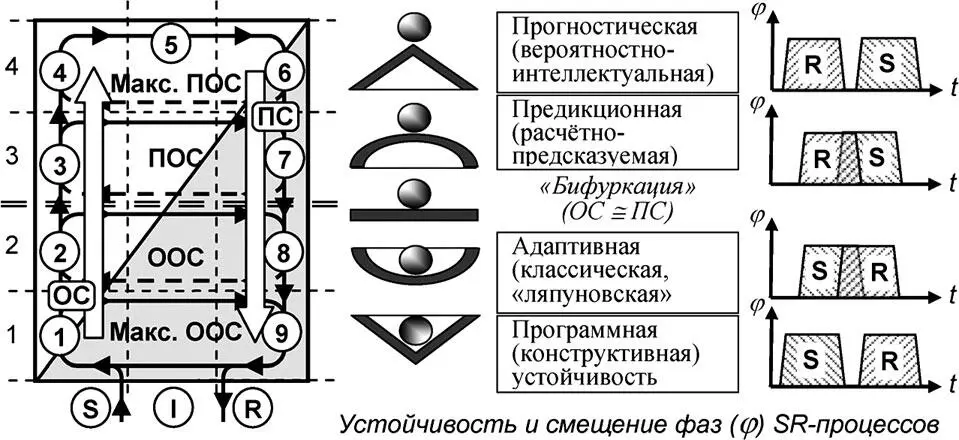
Рис. 6.11. Устойчивости и фазовые параметры систем управления 4U

В программном режиме выработка системой алгоритмики реакции R значительно отстаёт от появления инициирующих стимулов S. то есть, любой из возможных стимулов S вместе с алгоритмикой отработки в виде реакции R введён в работающую систему заранее, до возникновения в рабочем режиме. Для модели отработки колебательных и/или импульсных процессов можно сказать, что фаза R отстаёт от фазы S (или, что эквивалентно, фаза S опережает фазу R). Поскольку программа работы закладывается в систему заранее, на основании прошлого опыта взаимодействия подобных систем с внешней средой, то можно сказать, что программная схема управления охвачена почти 100-процентной ООС.