Сергей Авдошин - Информатизация бизнеса. Управление рисками

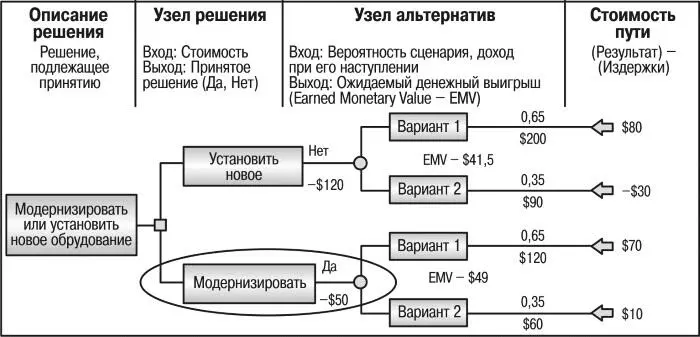
Рис. 15. Пример дерева решений

При построении дерева решений рассчитывается ожидаемая денежная стоимость для каждого из рассматриваемых вариантов (EMV – Expected Mone-tary Value). Если дерево содержит большое количество альтернативных решений, можно оценивать только наиболее приоритетные ветви. Ожидаемая денежная стоимость считается для одного или нескольких вариантов решений по следующей формуле:

EMV= Вероятность исхода1 × Стоимость исхода1 + Вероятность исхода2 × Стоимость исхода2 + … + Вероятность исхода(n) × Стоимость исхода(n).

Рассчитаем EMV для примера на рис. 13 по формуле EMV = (Доход – Расход) × Вероятность + (Доход – Расход) × Вероятность. Получим следующие значения:

EMV (Новое оборудование) = (200–120) × 0,65 + (90 – 120) × 0,35 = 41,5. EMV (Модернизация) = (120 – 50) × 0,65 + (60–50) × 0,35 = 49.

Далее выбирается вариант максимального EMV.

Метод деревьев решений позволяет специалисту определить оптимальную последовательность действий с учетом личных оценок и предпочтений. Ограничением практического применения данного метода является исходная предпосылка о том, что проект ИТ должен иметь обозримое или разумное число стратегий, а также слишком большая субъективность оценок вероятностей. Метод может быть полезен в ситуациях, когда решения, принимаемые в каждый момент времени, сильно зависят от решений, принятых ранее, и, в свою очередь, определяют сценарии дальнейшего развития событий.

В результате построения диаграммы дерева решений:

• выявляются важные (узловые) события и представляются в графическом виде;

• отражаются вероятности и величины затрат и выгод каждой логической цепи событий и будущих решений;

• используется анализ ожидаемой денежной стоимости для определения относительной стоимости альтернативных операций.

Для анализа рисков стоимости и расписания рекомендуется применять моделирование, так как оно обладает большей мощностью и снижает вероятность неправильного применения по сравнению с анализом ожидаемой денежной стоимости.

5. Моделирование и имитация. Имитационное моделирование – техника численных экспериментов, с помощью которых можно получить эмпирические оценки степени влияния различных факторов – исходных величин, которые точно не определены, на зависящие от них результаты – показатели.

Имитационное моделирование часто используется для количественной оценки воздействия изменений значений параметров системы (например, в случае наступления рискового события) на выбранные показатели (группу показателей) успешности проекта. Для проведения моделирования критичным является выбор или разработка математической модели, наиболее точно имитирующей поведение оцениваемого показателя.

Самый распространенный метод имитационного моделирования Монте-Карло дает наиболее точные и обоснованные оценки вероятностей при наименьших трудозатратах по сравнению с прочими методами, однако точность оценок в значительной степени зависит от качества исходных предположений и учета взаимосвязей переменных внешней среды. Современные программные средства позволяют учесть форму распределения вероятностей и корреляции десятков внешних переменных, однако оценить эти значения в практическом исследовании обычно достаточно непросто.

Упрощенный алгоритм моделирования Монте-Карло состоит из следующих шагов.

1. Задаются границы изменения параметра (факторов). При имитационных прогонах переменная выбирается случайным образом в соответствии с типом распределения и в границах заданного диапазона.

2. С помощью компьютерной программы, имитирующей случайность процессов, случайным образом выбираются значения параметра из заданного интервала и рассчитывается значение события. Значение рассчитывается исходя из выбранного распределения для ключевых параметров модели. Выбор распределения осуществляется либо по прошлой информации (статистические данные), либо по оценкам экспертов.

3. Проводится большое число прогонов, что позволяет получить множество случайных значений события, для которых могут быть рассчитаны среднее значение и стандартное отклонение (d). Каждый прогон происходит с вероятностью Р = 100/N (размер выборки). Для получения вероятности всех прогонов полученную величину Р умножаем на количество прогонов (с получением анализируемого результата).

4. Применяется правило трех сигм (при предположении о нормальности распределения вероятности), при котором значение окажется в трех интервалах:

• с вероятностью 0,68 в диапазоне ±1d);

• с вероятностью 0, 95 в диапазоне (±2d);

• с вероятностью 0, 99 в диапазоне (±3d).

Таким образом, обещая клиенту, что мы закончим проект в срок, соответствующий точке наиболее вероятного значения, мы имеем 50-процентную возможность окончить проект позднее обещанной даты (при выборе нормального распределения).

5. На основе полученных результатов принимается решение о целесообразности дальнейших действий при заданных параметрах. Например, если с вероятностью более 0,94 нижняя граница оценки проекта положительна, то проект рассматривается как проект низкого риска для заданного фактора риска.

В результате моделирования получается диаграмма, показывающая вероятности всех возможных сроков завершения проекта и вероятности возможных затрат с четким изображением наиболее вероятных затрат по проекту (рис. 16, 17).

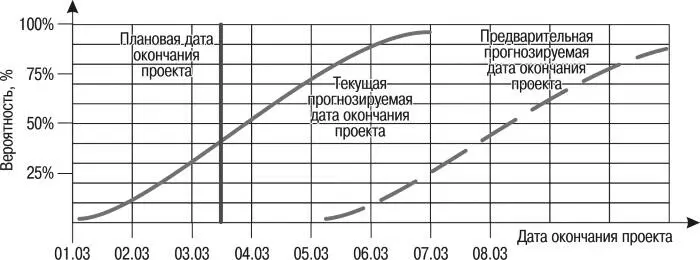
Рис. 16. Прогноз даты завершения проекта на основании количественной оценки риска

Рис. 17. Прогноз суммарной стоимости проекта на основании количественной оценки риска

Практическое применение метода Монте-Карло продемонстрировало широкие возможности его использования, особенно в условиях неопределенности и риска. Моделирование дает более точные оценки, чем другие методы, например анализ сценариев, что обусловлено перебором промежуточных вариантов. Данный метод особенно удобен для практического применения тем, что удачно сочетается с другими экономико-статистическими методами, а также с теорией игр и другими методами исследования операций.

Однако для использования этого метода необходим большой объем исходной информации, основанной на анализе статистических данных. Вероятностные распределения различаются по каждой позиции и меняются со временем, некоторые составляющие зависят от развития в предыдущих периодах (условная вероятность), существует вероятность появления определенной последовательности статистических данных (появления ошибок, прочего). Точность предоставленных данных и прогнозных оценок напрямую повлияет на качество моделирования.