Роман Акентьев - Финансовая грамотность, или Основы управления личными финансами

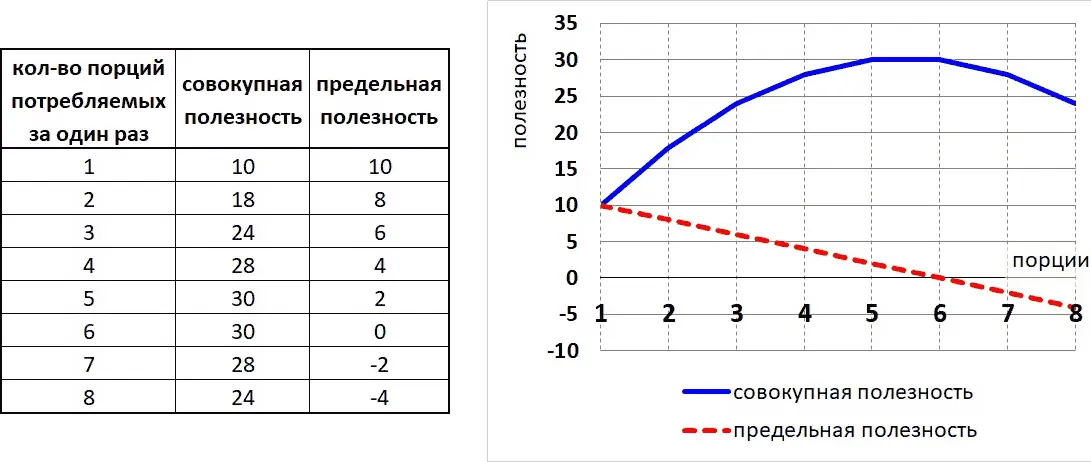
Рисунок 6. Графическое представление совокупной и предельной полезности.

Полезность товара или услуги для каждого человека имеет свою некоторую количественную границу, преодолевая которую, полезность перестаёт расти (то есть приносить удовольствие человеку от потребления данного товара или услуги) и даже может становиться отрицательной. Из определения предельной полезности вытекает формулировка закона убывающей предельной полезности, который гласит:

« По мере увеличения количества потребляемого товара его предельная полезность имеет тенденцию к сокращению ». [22] Этот закон обычно называют первым законом Госсена (по имени немецкого экономиста Германа Госсена впервые определившего идею убывающей предельной полезности в 1854 г.)

Если каждая последующая единица блага обладает все меньшей и меньшей предельной полезностью, то потребитель будет покупать дополнительные единицы блага лишь при условии снижения их цены. Приобретая одни товары, потребители жертвуют потреблением других. Поэтому выбор потребителя в условиях рыночной экономики всегда связан не только с оценкой полезности потребляемых благ, но и с сопоставлением цен альтернативных товаров.

Кривая предельной полезности показывает, что полезность потребляемых одна за другой единиц блага постепенно убывает, поскольку растет степень удовлетворения потребителя. Если предельная полезность равна нулю, следовательно, данное благо существует в количестве, которое может полностью удовлетворить данную потребность.

Но фактически измерить полезность всё-таки нельзя (как, например, килограммы для веса, метры для расстояния и т.д.), в силу того, как мы уже знаем, что полезность является субъективным показателем. Потребитель оценивает не полезность отдельных благ, а наборов благ, то есть потребитель не может точно сказать насколько для него хлеб полезней молока. Но потребитель может сказать, что для него полезнее будет два литра молока и одна булка хлеба (потребительский набор № 1) нежели чем две булки хлеба и один литр молока (потребительский набор № 2).

Поэтому возникла альтернативная ординалистская теория полезности.

Ординалистская (порядковая) теория полезности , основывается на том, что предпочтения потребителя относительно предлагаемых к выбору альтернатив не могут измеряться количественно, а только сравниваться. Потребитель выбирает – эта альтернатива хуже или лучше другой?

Согласно этой теории, невозможно измерить предельную полезность, так как потребитель измеряет не полезность отдельных благ, а полезность наборов благ. Предполагается, что измерению поддаётся порядок предпочтения наборов благ. Более глубокое объяснение поведение потребителя, когда он стремится максимизировать полезность, получаемую от приобретения двух товаров (разных благ) в условиях ограниченного бюджета, даётся при помощи кривой безразличия и бюджетной линии.

• Кривая безразличия– это множество всевозможных комбинаций благ, имеющих для потребителя одинаковую полезность, то есть потребителю безразлично какой набор товаров выбрать;

• Бюджетная линия(линия бюджетных ограничений) – показывает различные комбинации двух благ, которые потребитель может приобрести, при данном доходе и данных ценах.

Равновесие потребителя достигается, когда при определенных ценах и уровне дохода потребитель получает максимальную полезность от потребления набора товаров. В этой точке наклон бюджетной линии и кривой безразличия совпадает.

Чтобы подробнее ознакомиться с этими теориями, автор рекомендует читателю обратиться к специализированной литературе.

В 1738 году Даниил Бернулли предложил объяснение так называемого Санкт-Петербургского парадокса, иллюстрирующего расхождение между теоретически оптимальным поведением человека (игрока) и «здравым смыслом». Этот парадокс возник как математический казус и попытка найти всеобщий принцип (правило) принятия решений в условиях неопределённостей . Этот парадокс неявно сыграл важную роль в развитии экономических теорий и стал предтечей теории ожидаемой полезности.

Суть парадокса в следующем. Предлагается следующая игра: подбрасывается монетка до первого выпадения орла. По итогам игры выплачивается выигрыш в размере 2 N-1руб., где N – номер броска, на котором выпадет орёл.

Вопрос: сколько бы вы заплатили за участие в такой игре? Или, в другой формулировке, при каком вступительном взносе игра становится выгодной (то есть игрок выиграет больше, чем заплатит)?

При каждом подбрасывании вероятность выпадения орла 1/2 или 0,5 (так как монетка выпадет либо орлом, либо решкой). При этом предыдущий результат подбрасывания не оказывает влияние на результат последующего подбрасывания. Каждое подбрасывание независимо друг от друга. Если орёл выпадает при первом броске, то выигрыш составит 1 рубль. Если орёл выпадает при втором броске, то выигрыш составит 2 рубль. Если орёл выпадает при третьем броске, то выигрыш составит 4 рубля. При четвёртом – 8 рубля и т.д. Другими словами, выигрыш, возрастая от броска к броску вдвое, последовательно пробегает степени двойки – 1, 2, 4, 8, 16, 32 и так далее.

Другими словами, подходящим математическим описанием данной ситуации, является случайная величина х, принимающая значения × = 2 N-1, с вероятностью р = 2 -N. Требуется найти значение, которое в определённом смысле эквивалентно указанной величине. В качестве такого эквивалента случайных величин (в данном случае цена участия в игре) используют математическое ожидание (как справедливую цену азартной игры). Математическое ожиданиеесть среднее значение случайной величины, которая считается по следующей формуле:

М(х) = р 1х 1+ р 2х 2+ … р nх n,

где р 1, р 2, …р n– вероятность каждого исхода, х 1, х 2, …х n– значение каждого исхода.

Математическое ожидание выигрыша:

• N=1 (при первом подбрасывания составляет), р 1х 1= 2 -N* 2 N-1= 0,5*2 0= 0,5 руб.;

• N=2 (при втором подбрасывания составляет), р 2х 2= 2 -N* 2 N-1= 0,25*2 1= 0,5 руб.;

• N=3(при третьем подбрасывания составляет), р 3х 3= 2 -N* 2 N-1= 0,125*2 2= 0,5 руб.;

• И т.д.

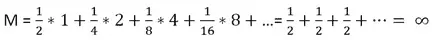
Как видим, для данной задачи математическое ожидание выигрыша бесконечно.

Это означает, что формально игрок может получить бесконечно большой выигрыш, однако большинство людей уклонится от участия в такой игре. Именно по этой причине и используется слово «парадокс» в названии задачи.