Саманта Клейнберг - Почему

Для менее экстремального случая, скажем, мы подбросим монету 10 раз, и выпадут 9 орлов и 1 решка.

P -значение такого результата (здесь нулевая гипотеза – что монета симметрична, а альтернативная – что она смещена в любом направлении) – это вероятность тех самых 9 орлов и 1 решки + вероятность 9 решек и 1 орла + вероятность 10 орлов + вероятность 10 решек [137]. Причина, по которой сюда включены две серии со всеми орлами и всеми решками, в том, что мы рассчитываем вероятность события как минимум такого же экстремального, как и наблюдаемое, а эти серии – самые экстремальные. Наша альтернативная гипотеза – смещение монеты в любом направлении, а не просто в сторону орлов или решек; вот почему мы включили длинные серии решек.

На рис. 3.6 представлены гистограммы для орлов в серии из 10 бросков по 10 монет. Если бы результатом для каждой монеты было в точности 5 орлов и 5 решек, каждый график представлял бы одну черту длиной 10 пунктов с центром на отметке 5. Но в реальности случаются и б о льшие, и меньшие значения, и даже одна серия из всех решек (показанная маленькой чертой, которая пересекает один график справа налево).

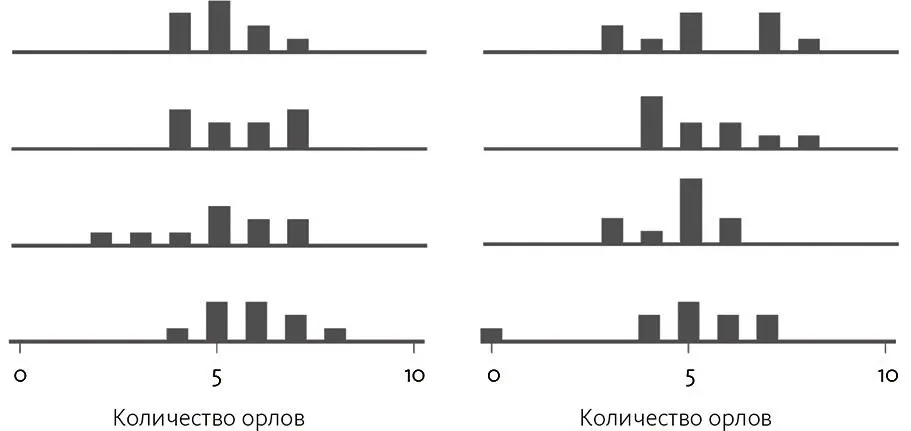
Рис. 3.6.Каждая гистограмма представляет эксперимент, где 10 монет подбрасывают 10 раз. Каждая серия из 10 монет образует точку данных на графике в зависимости от количества орлов. Показано 8 примерных экспериментов

Такое событие все равно невероятно при наличии одной симметричной монеты; но что будет, если мы подбросим 100 монет? Увеличивая число экспериментов, мы создаем больше возможностей, чтобы некое по видимости аномальное событие произошло случайно. К примеру, вероятность того, что конкретный человек выиграет в лотерею, на самом деле мала; но, если играют достаточно людей, можно гарантировать, что кто-нибудь победит. На рис. 3.7 показана такая же гистограмма, но уже для 100 монет. Действительно, будет странно, если мы не увидим как минимум одной серии из 9 или более орлов или решек, когда бросают так много монет (или лотерею, где не будет победителей, если шансы 1: 1 000 000, а играют 100 000 000 человек).

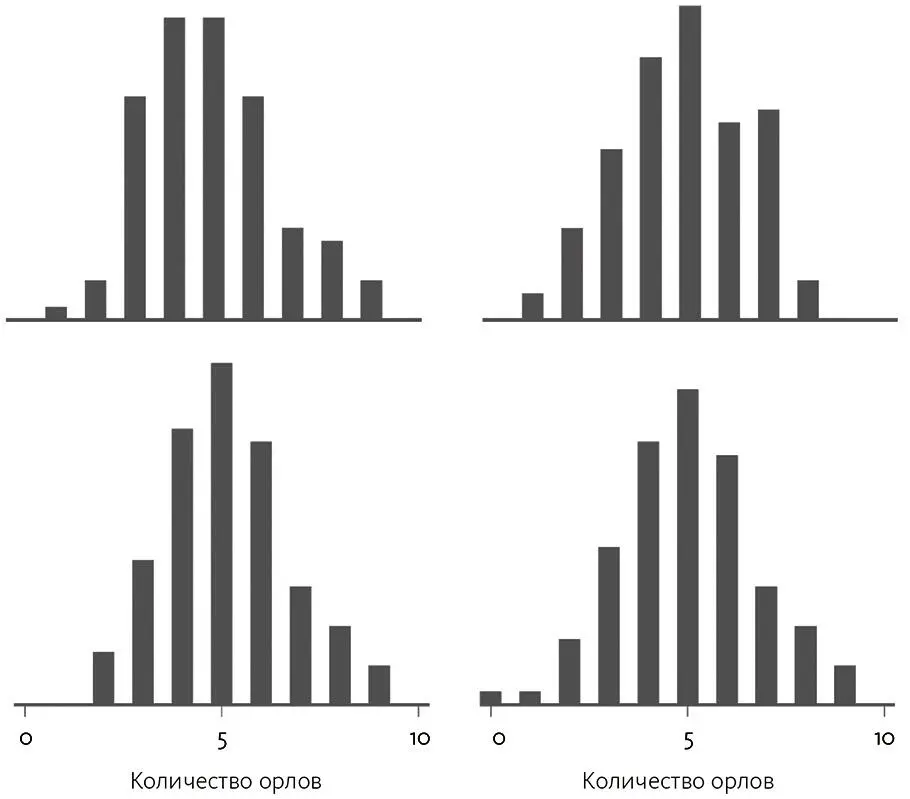
Рис. 3.7.Результаты подбрасывания 100 монет по 10 раз для каждой. Показано 4 эксперимента

Именно проблема одновременного проведения многочисленных тестов и оказалась во главе угла исследования МРТ, с рассказа о котором мы начали разговор. Проверке подверглись тысячи малых областей мозга (а в исследованиях на людях их еще больше, потому что человеческий мозг включает множество областей), поэтому совсем неудивительно, что одна из них продемонстрировала значительный кровоток. Проблемы такого вида именуются проверкой многомерной гипотезы , что означает одновременную проверку большого количества гипотез. Вопрос становится еще более существенным с появлением нового метода, генерирующего громадные наборы информации (например, множества МРТ и экспрессии генов) с так называемыми большими данными. Ранее было возможно в рамках одного эксперимента проверить только одну гипотезу, теперь же, когда мы способны анализировать тысячи переменных, неудивительно, что между ними обнаруживаются корреляции в силу количества проведенных тестов.

В эксперименте с лососем ученые протестировали тысячи гипотез, и каждая утверждала, что некая область мозга проявит значительную активность.

В действительности же исследование доказало: все эти тесты могут дать кажущиеся значимыми результаты по чистой случайности. Было показано, что при использовании статистических методов, корректных для множества сравнений (фактически каждый тест требует более жесткого порогового показателя), значимой активности выявлено не было даже при очень нежестких порогах p -значений [138].

Важная вещь, которую стоит запомнить: читая отчет о некой необходимой находке, которая была взята из громадного набора одновременных тестов, обязательно обращайте внимание на то, как авторы решают проблему множественного сравнения. Статистики расходятся во мнении, как именно (и когда) корректировать этот фактор, но все дебаты в целом сводятся к тому, какой тип ошибки хуже. Корректируя множество сравнений, мы, по сути, заявляем о желании снизить количество ложных открытий и готовы мириться с возможностью пропустить из-за этого некие значимые находки (и генерировать ложноотрицательные результаты). С другой стороны, выступая против поправок, заявляем о нежелании упускать истинно положительные результаты за счет нескольких ложных открытий.

Между этими двумя типами ошибок всегда идет поиск компромисса, а предпочтения зависят от индивидуальных целей [139]. Возможно, для эксплораторного анализа, где поиск ведется экспериментальным образом до получения конечного результата, мы считаем нужным, образно говоря, раскинуть обширную сеть. С другой стороны, если мы стараемся отобрать узкоцелевую группу кандидатов для разработки дорогостоящего препарата, каждое ложное умозаключение способно привести к массе впустую потраченного времени и средств.

Мы часто спорим, почему корреляция может не иметь причинного характера, но важно признать, что также могут существовать истинные причинные взаимосвязи без видимого соотношения. То есть корреляцию нельзя считать демонстрацией причинности, и выявление взаимосвязи также не необходимое условие причинности.

Известен пример, именуемый парадоксом Симпсона (мы поговорим о нем в главе 5). В общем, даже если в рамках неких подгрупп есть взаимосвязь (скажем, тестируемый препарат в сравнении с известным лекарством улучшает результаты у некой группы населения), мы можем не обнаружить зависимости или найти, но обратную, если подгруппы объединить. Если новый препарат больше используют пациенты в наиболее тяжелом состоянии, а те, кто чувствует себя лучше, чаще получают обычное лекарство, то, если не принимать во внимание серьезность заболевания, может показаться, что тестовое лекарство приводит к худшим результатам для населения.

В качестве еще одного примера причинности без корреляции рассмотрим влияние длительных пробежек на вес. Да, пробежки могут снижать вес за счет траты калорий, но бег также приводит к повышению аппетита, что, в свою очередь, ведет к увеличению веса (и, таким образом, отрицательно влияет на его потерю). В зависимости от силы каждого конкретного воздействия или исследуемых данных положительный эффект пробежек может полностью нивелироваться отрицательным, а значит, между бегом и потерей веса соотношения не будет. Структура этого примера представлена на рис. 3.8. Причина обладает положительными и отрицательными воздействиями, которые осуществляются различными путями; вот почему мы можем либо не наблюдать корреляции вообще, либо наблюдать нечто близкое к ней (вспомним: любые меры не абсолютны).