Александр Бакулин - Гравитация и эфир

То есть в момент рождения электромагнетизма каждую частицу – «квант эфира» надо считать супер-релятивистской, энергия которой на много порядков там превышает энергию сегодняшней частицы эфира. Энергия такой супер-релятивистской частицы целиком и полностью определяется только энергией вращательного движения такой частицы:

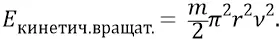
Эту нашу фундаментальную формулу «механической» энергии тела – волчка, пожалуй, можно с успехом применять для скоростей частицы, на порядки превышающих скорость света. Но как оценить – насколько всё же возрастает энергия электромагнитной частицы при её «гравитационной» скорости? Для начала определим, причём предельно точно определим, по классической формуле, энергию переноса центра масс частицы эфира – как кинетическую энергию её поступательного движения, в предположении движения частицы с максимально возможной, то есть с «гравитационной» скоростью:

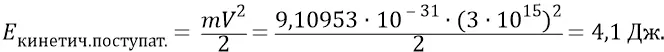
Теперь обратимся к аналогиям. В главе «Масса физического тела» мы чётко, вслед за физиками, утверждаем, что для элементарных электромагнитных частиц зона релятивизма начинается с их энергий порядка 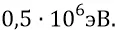При такой энергии, как мы там показываем, энергия вращательного движения частицы, возрастая, сначала сравнивается с кинетической энергией поступательного движения частицы, а затем, при дальнейшем ускорении, она резко уходит вперёд. Причём даже физики в их ускорителях подбираются к энергиям на 6 порядков более высоким, доводя их, допустим, до величины 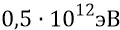. Но это справедливо для частиц, ускоряемых электромагнитным полем до скоростей почти равных световым – «предельным для электромагнетизма».

Но у нас частицу ускоряет не электромагнетизм, но гравитация. Вопрос: может ли гравитация, по аналогии, увеличить энергию вращательного движения электромагнитной частицы на те же, допустим, 6 порядков по отношению к энергии поступательного движения частицы при её скорости, близкой к скорости гравитации? А почему бы и нет? То есть сама по себе гравитация своими маленькими гравитационными квантами не умеет непосредственно раскручивать «гигантские» кольца электромагнитных частиц. Но мы говорим сейчас об области «сингулярности» (сингулярности для электромагнетизма) Большой Вселенной. Там только что рождённые электромагнитные частицы «кишат» – проходят друг сквозь друга чуть ли не сплошным потоком электромагнитных колец их конструкций. Нигде и никогда больше нельзя будет встретить в Жизни Вселенной такой большой плотности эфира, только что рождённого и разлетающегося от этой области почти со скоростью гравитации. То есть великая плотность направленного гравитационного поляв этой области сильно тянет каждую электромагнитную частицу «вперёд», пропихивая её через сплошной пространственный ряд электромагнитных колец других частиц. А это, в свою очередь, эквивалентно гигантскому, уже «электромагнитному» полю – как очень великому потоку взаимодействующих друг с другом электромагнитных частиц.

Остаётся только вопрос о том, сможет ли конструкция электромагнитной частицы выдержать бешеное вращение своих преонных колец, оставаясь целостной?

Итак, мы хотим теперь попытаться увеличить энергию такой частицы до некоторой почти максимально возможной для электромагнетизма, например, увеличить её до величины:

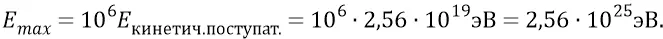
Про такие энергии даже наши физики не говорят. В джоулях это будет:

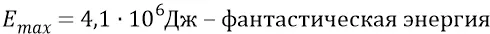
единичной элементарной электромагнитной частицы типа электрона или кванта вакуума.

Доверимся нашей фундаментальной формуле и попробуем оценить частоту вращения такой фантастической частицы:

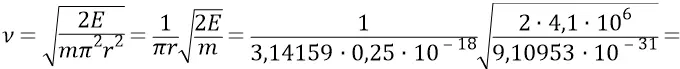
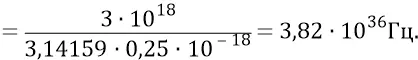
Порядок этой частоты не слишком сильно пугает нас.

Снова обратимся к аналогиям: будем сравнивать орбитальные вращения электрона в атоме и преона на электромагнитной орбите элементарной частицы. Электрон на орбите, при собственной там частоте порядка 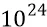Гц, делает за секунду порядка 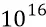оборотов по орбите, успевая вращаться, следовательно, 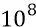раз вокруг своей оси на каждом обороте по орбите. Если преон на орбите кольца конструкции частицы делает такое же количество оборотов, то его собственная частота:

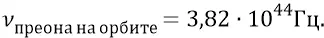
При этом частота тех преонов, которые мы называем «преонами привязки» и которые держат орбитальные преоны на нитках их электромагнитных орбит в частице, определяется длиной волны такого преона, делающего на диаметре частицы полный оборот вокруг своей оси:

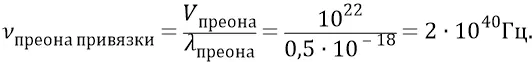
Размер (диаметр кольца) преона – 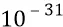м. При частоте вращения электромагнитного кольца частицы – 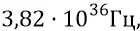время такого обращения:

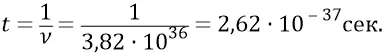
Длина окружности преонной орбиты электромагнитной частицы:

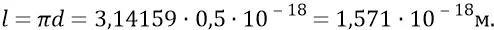
На этой длине разместятся «один к одному»

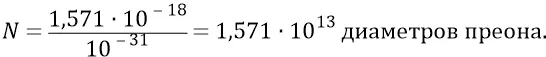
Точным попаданием преона привязки поля ядра частицы на орбитальный преон будем считать промах не больший одной тысячной диаметра преона. Тогда при каждом угле сдвига плоскости поляризации кольца конструкции частицы, при её собственном вращении, мы насчитаем 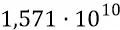точных попаданий преонов поля ядра частицы для каждого угла сдвига плоскости поляризации и для каждой хорды орбиты в её азимутальном положении на орбите. То есть при таком соотношении частот вращений кольца и попаданий по нему поля ядра мы будем иметь 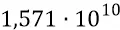хорд орбиты, что вполне достаточно для удержания преона на орбите частицы.