Александр Бакулин - Гравитация и эфир

Таким образом, найденная нами собственная частота вращения электромагнитной частицы – 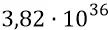Гц является вполне допустимой для такой частицы. А следовательно, является вполне допустимой и реальной энергия такой «релятивистской» частицы:

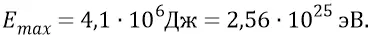
Найдём инертную массу такой частицы из стандартного выражения для релятивистской энергии:

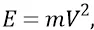
где V в данном случае – гравитационная скорость – 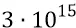м/сек;

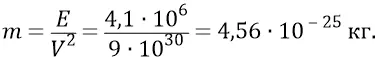
Тогда количество движения такой «начальной» частицы Вселенной:

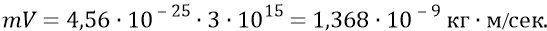
Итак, в первичном Вихре Вселенной закручены гравитационные частицы, линейная скорость которых практически равна скорости движения гравитационного кванта. Эти гравитационные частицы являются, по отношению к гравитационным квантам, релятивистскими.

В нашей философии мы приходим к некоторой стандартной методике оценки энергии и инерционной массы любых «релятивистских» частиц: как электромагнитных, так и гравитационных. «Релятивистская» – это та частица, кинетическая энергия вращательного движения которой сравнима или больше кинетической энергии поступательного её движения.

Кинетическая энергия поступательного движения гравитационной частицы (гравитационного ядра будущей электромагнитной частицы):

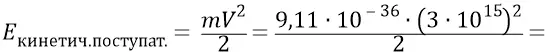
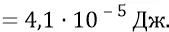
Далее мы уже предположили, что в гравитационной Эфирке при максимальной закрутке Вихря, перед самым Большим Взрывом, все гравитационные частицы обязаны там быть не просто релятивистскими, но супер-релятивистскими. За счёт сильного вращения вокруг собственных осей энергия таких частиц вполне может достигать 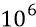– 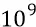величин кинетической энергии поступательного движения частиц. Если, для примера, принять верхний предел возрастания энергии порядка 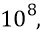то кинетическая энергия вращательного движения частицы (она же – полная энергия супер-релятивистской частицы):

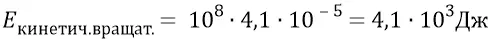
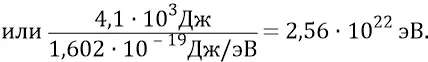
Инерционную массу такой гравитационной частицы найдём из стандартной релятивистской формулы:

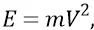
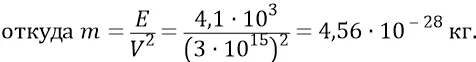
Тогда количество движения такой гравитационной частицы:

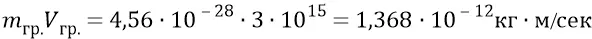
Оценим порядок собственной частоты вращения такой частицы:

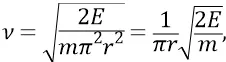
где r – радиус конструкции гравитационной частицы – 0,25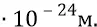

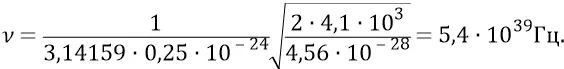
При рождении электромагнитной частицы первичная конструкция гравитационной частицы (как зародыш электромагнитной) получает инерционный удар. Мы определили, что рождающаяся электромагнитная частица вполне выдержит частоту собственного вращения, на 3 порядка меньшую найденной нами только что гравитационной. То есть пусть частота вращения электромагнитной будет:

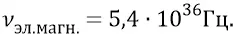
Тогда определим энергию такой супер-релятивистской электромагнитной частицы:

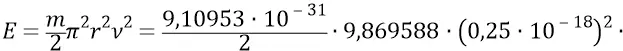
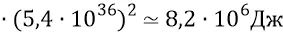
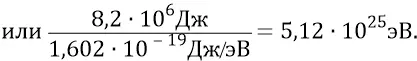
Инерционную массу электромагнитной частицы либо её скорость можно было бы найти из стандартной релятивистской формулы:

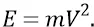
Однако перед нами – уравнение с двумя неизвестными, то есть полнейшая неопределённость. Поэтому нам придётся выбрать одну из величин. Само явление инерционного удара может предполагать какое-то резкое замедление скорости рождающейся электромагнитной частицы по отношению к скорости первичной, равной 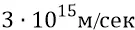. Но у нас есть второе уравнение с теми же двумя неизвестными величинами:

Из этого второго уравнения выразим, допустим, инерционную массу рождающейся электромагнитной частицы через её скорость:

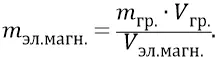
Подставим это выражение в первое уравнение:

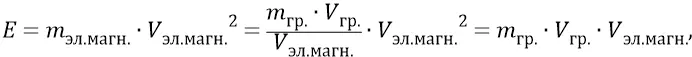
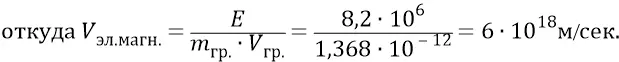
Мы видим, что полученная скорость в 2000 раз превышает гравитационную скорость – 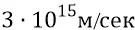. Но здравый смысл состоит в том, что электромагнитная частица не может получить скорость, большую скорости первичной частицы. Это следует из того, что нитка электромагнитной орбиты новой частицы накручивается на гравитационное ядро ровно поперёк скорости движения первичной. Поперечные моменты количеств движения не могут привести к возрастанию имеющейся скорости. Поэтому мы можем принять скорость электромагнитной частицы максимально возможной, но соответствующей здравому смыслу. Такой скоростью будет принятая нами скорость гравитации – 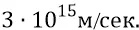Тогда инерционную массу электромагнитной частицы найдём, допустим, из выражения