Алексей Куприн - Слово о карте

На картах обычно дается не только численный, но и линейный масштаб в виде графической шкалы. Понятно, что для карты определенного масштаба строят соответствующую шкалу. Но можно построить и один график для карт разных масштабов.

Проведем две взаимно перпендикулярные линии и отложим по вертикальной оси вверх отрезок ВС , равный 10 см, а по горизонтальной оси влево — отрезок ВА , равный 2,5 см (рис. 19).

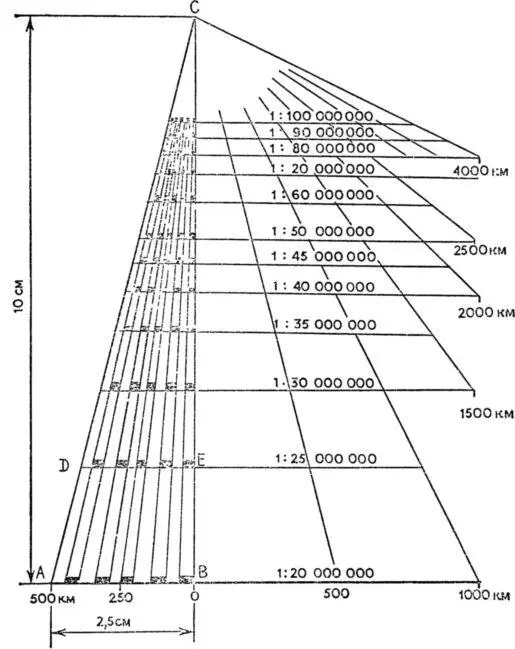
Рис. 19. Универсальный масштаб.

Этот последний отрезок будем считать основанием линейного масштаба для карты 1:20 000 000. В этом масштабе он будет соответствовать 500 км. Чтобы найти расстояние СЕ, от которого нужно отложить основание следующего масштаба (1:25 000 000), пользуются соотношением, полученным из подобия треугольников АВС и ADE :

СВ/CE = АВ/DE; CE = CB·DE/AB = 10DE/2,5 = 4DE .

Величина DE — основание линейного масштаба — для карты 1:25 000 000 соответственно будет равна 2 см (500 км:25 000 000), значит 8 см. Так же рассчитывают расстояния от точки С до линий, где будут строиться основания линейных масштабов других карт.

Построенный график можно использовать не только для измерения расстояний по картам разных масштабов, но и для определения среднего масштаба по любому меридиану и любой параллели. Масштаб карты по меридиану определяют в следующем порядке. Раствор циркуля-измерителя, соответствующий отрезку меридиана с разностью широт 5 или 10°, будем вести по нашему масштабу вдоль наклонных линий до тех пор, пока он не уложится в расстояние 555 км для 5° или расстояние 1110 км для 10° на какой-либо горизонтальной линии. Масштаб, подписанный над этой линией, будет соответствовать среднему масштабу карты по данному меридиану. Например, отрезок MN , снятый с карты по меридиану с разностью широт 10°, уложился в расстояние 1110 км по линии масштаба 1:40 000 000. Таков и будет средний масштаб карты в данном направлении.

Чтобы определить масштаб карты по параллели, нужно вначале найти по приведенной выше таблице длину дуги параллели в 5 или 10° на определенной широте, а затем порядок действий будет тот же, что и при определении масштаба карты по меридиану.

Перед вами глобус. Как по нему составить карту какого-либо материка, допустим, Африки? Прежде всего выберем проекцию и построим соответствующую ей картографическую сетку в определенном масштабе. Возьмем наиболее простую проекцию — квадратную. На листе бумаги проведем две взаимно перпендикулярные линии. Вертикальную линию будем считать нулевым меридианом, а горизонтальную — экватором. Через равные интервалы проведем параллельные им линии, образующие квадраты. Стороны квадратов, т. е. расстояния между параллельными линиями, зависят от оцифровки параллелей и меридианов и масштаба карты. Предположим, мы хотим составить карту в масштабе 1:50 000 000 (по экватору и меридианам) с густотой картографической сетки 10°. В таком случае сторона квадрата составит 2,22 см (1110 км:50 000 000).

Пользуясь вычерченной сеткой параллелей и меридианов, перенесем с глобуса по соответствующим клеткам контур береговой линии африканского материка.

В пределах каждой клетки рисунок переносится на глаз. Чтобы береговая линия не была ломаной, нужно вначале наметить точки ее пересечения со сторонами клетки, а затем их соединять, учитывая общий изгиб линии.

По картографической сетке можно проверить правильность перенесения береговой линии на карту путем сличения координат соответствующих точек. Так, координаты крайних точек Африки следующие: северной — мыс Эль-Абьяд (37° с. ш., 10° в. д.); южной — мыс Игольный (35° ю. ш., 20° в. д.); западной — мыс Альмади (18° з. д., 15° с. ш.); восточной — мыс Хафун (51° в. д., 10° с. ш.)

Составим еще одну карту — карту Австралии в цилиндрической проекции, но за основу возьмем не глобус, а карту восточного полушария (рис 20, а).

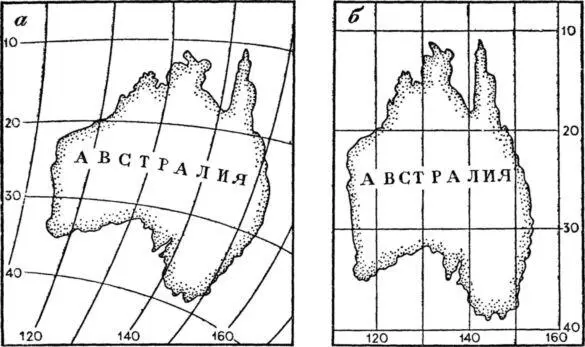
Рис. 20. Изображение Австралии на карте полушария (а) и на карте в цилиндрической проекции (б).

Картографическая сетка для нашей карты будет прямоугольной с соотношением сторон клеток 1:2, например, отрезок меридиана в 10° широты будет соответствовать 2 см, а параллели в 10° широты — 1 см. Вычертим рамку карты, и у ее сторон подпишем широты и долготы у соответствующих параллелей и меридианов (рис. 20, 6). Контур материка будем переносить более точно — по опорным пунктам. Для этого на исходной карте определим координаты точек пересечения береговой линии с меридианами или параллелями и направление береговой линии в этих точках (табл. 2).

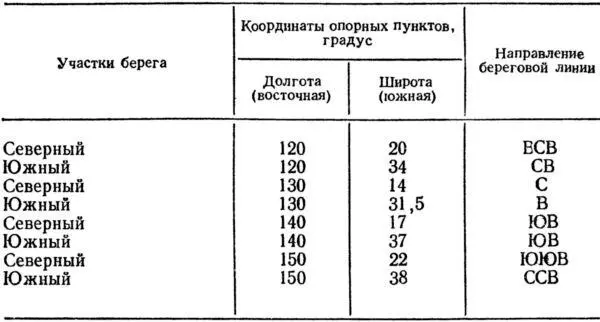
По координатам нанесем на картографическую сетку опорные пункты и от них на глаз перенесем береговую линию со всеми ее изгибами. Опорные пункты дают возможность более точно перенести с исходной карты контур материка на карту, составляемую в другой проекции.

Сравните очертания Австралии в обеих проекциях. Если в первой проекции (см. рис. 20, а) общий вид материка примерно соответствует действительной конфигурации, то во второй проекции (рис. 20, 6) изображение получилось сжатым по долготе и вытянутым по широте. И тем не менее в обеих проекциях очертание береговой линии со всеми ее подробностями остается постоянным и географические координаты каждого ее изгиба будут одинаковыми.

Приведем еще пример преобразования одной картографической проекции в другую. Исходной картой будет карта СССР в конической проекции (рис. 21, a), a по ней нам нужно составить такую же карту, но в цилиндрической проекции (рис. 21, 6).

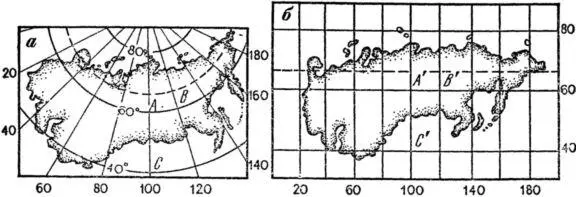
Рис. 21. Карта СССР в конической (а) и цилиндрической (б) проекциях.

Здесь по сути дела задача сводится к тому, чтобы растянуть дуги параллелей в прямые линии. А практически решается она так. Нанесем параллельно друг другу три прямые линии, которые обозначают параллели 40, 60 и 80°. Расстояния между ними равны соответствующим расстояниям на исходной карте ( А'С' = АС ). На параллели 60° отложим отрезки между меридианами ( А'В' = АВ ) и от точек отложения проведем линии, перпендикулярные к параллелям. Они будут меридианами. На построенную картографическую сетку перенесем по клеткам сухопутные и морские границы страны. Можно уточнить их положение путем отложения одинаковых расстояний по меридианам от 60-й параллели.