Петр Путенихин - Радиус наблюдаемой Вселенной и горизонт Вселенной

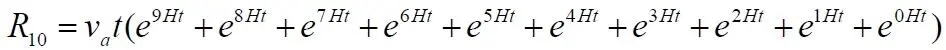
Для лучей видимости закономерности меняем последовательность слагаемых на противоположную:

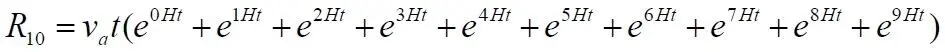
Закономерность очевидна, поэтому можем записать уравнение в общем виде для любого количества интервалов времени и числа слагаемых:

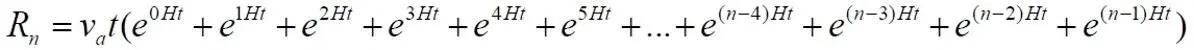
Рассмотрим особый случай: авто достигает конечной точки, финиша. Это значит, что рассматриваемое уравнение, сумма ряда будет равна увеличившейся по указанному закону исходной дистанции, растягивающейся трассы. Поскольку начальная удалённость финиша была S 0, то через время T она увеличится до значения:

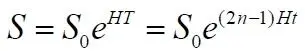
Рассматриваемое условие запишем в виде:

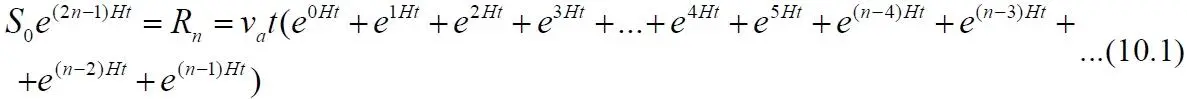
Перепишем правое равенство немного короче, в одну строку:

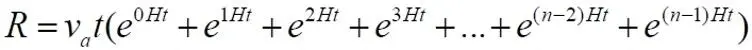
Для графических построений удобнее немного иная форма записи правой части уравнения, в виде, напоминающем исходное уравнение со множеством скобок. Для краткости оставим справа только слагаемые в скобках:

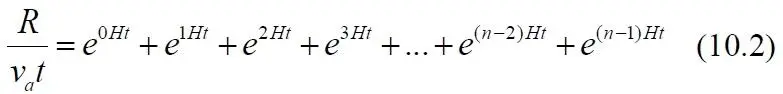
Теперь выделим последовательно множители в правой части

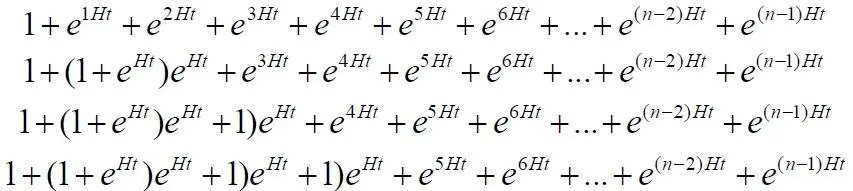
Замечаем закономерность и записываем окончательно:

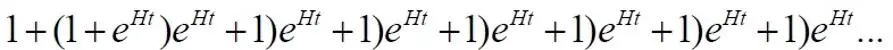
С множителем v at внутри скобок это уравнение имеет вид:

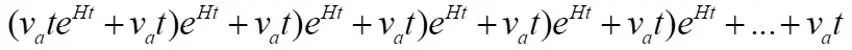
Для исключения ошибок, для проверки точности уравнения выполняем обратное действие, раскрываем скобки:

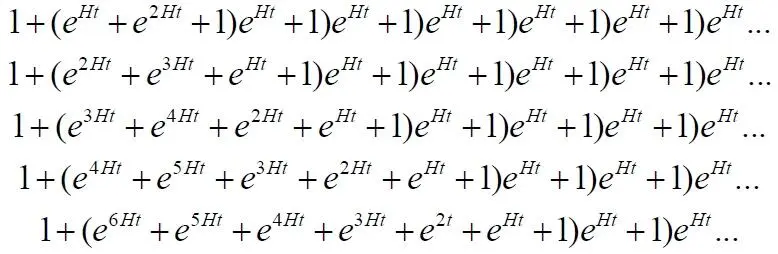
То же самое для уравнения с множителем v at внутри скобок:

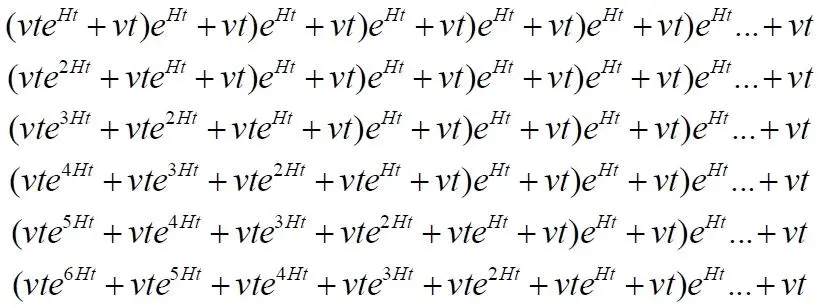
Видим, что последовательности явно ведут к верному результату. Однако для большей уверенности рассмотрим, как и выше, вариант с числом слагаемых n = 10:

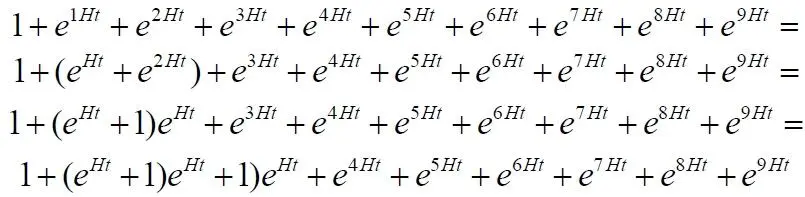
Вновь, заметив закономерность, записываем для n=10:

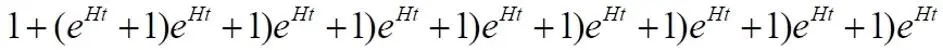
Проверяем ряд, как и ранее, раскрывая скобки:

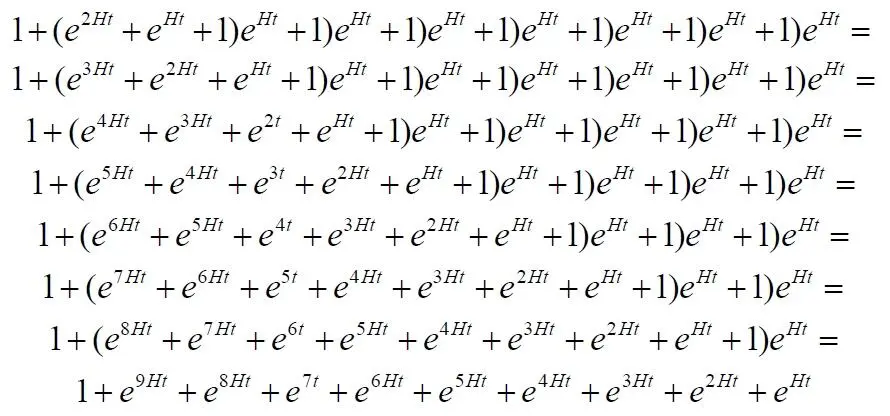
Сравниваем этот прямо и обратно преобразованный ряд с исходным рядом слагаемых (10.2):

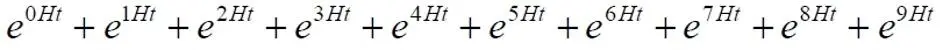
Видим, что эти ряды для n = 10 совпали, поэтому переписываем правую часть уравнения (10.2) в общем виде:

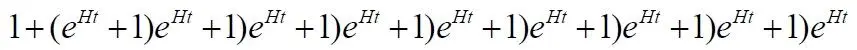
Или в полном виде:

Здесь число слагаемых (с учётом единичного слагаемого) равно 10. Для произвольного числа слагаемых уравнение (10.1) закономерно можно записать в следующем виде:

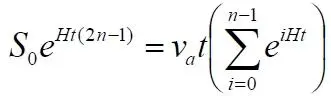
То же самое с множителем, внесённым в скобки:

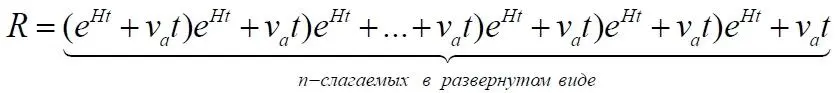
Мы рассматривали движение авто на вытягивающейся дорожке. Однако все приведённые рассуждения полностью соответствуют и движению фотона от некоторой сверхновой к Земле в расширяющемся пространстве Вселенной. Поэтому в итоговых уравнениях мы можем просто заменить скорость авто скоростью света:

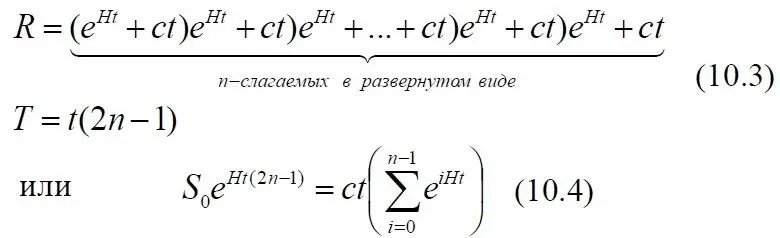
Уравнение (10.3) показывает действительную величину удалённости фотонов от сверхновой, равенство (10.4) отражает равенство этой удалённости и конечной удалённости Земли от сверхновой. Это условие мы заложили в постановке задачи. Но из них следует и провозглашённый в задаче вывод. Всё движение, и авто и фотонов, происходило в течение времени T, что соответствует, в свою очередь, длине пройденного пути с точки зрения движущегося объекта – авто или фотонов. Действительно, на спидометре авто за это время при заданной скорости будет показан вполне определённый пройденный им путь:

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.