Петр Путенихин - Радиус наблюдаемой Вселенной и горизонт Вселенной

Одним из основных результатов астрономических наблюдений являются красное смещение и яркость различных объектов во Вселенной. По этим данным определяют расстояние до наблюдаемого объекта и скорость его удаления. В отношении этих наблюдений в литературе часто упоминается обстоятельство, которое обычно формулируется как "взгляд в прошлое". Если некоторая галактика, сверхновая находится на большом удалении, свет от неё движется до Земли какое-то достаточно большое время. В момент получения наблюдателем этого света галактика находится уже на другом, большем удалении, чем в момент вспышки. Возникает закономерный вопрос: что следует принять за "удалённость галактики"?

Очевидны три варианта. Первый вариант – удалённость сверхновой в момент вспышки. Эту удалённость и следует считать действительной, наблюдаемой её удалённостью, хотя и определённую с задержкой во времени. Вариант второй – удалённость галактики в момент получения света на Земле, то есть, удалённость после увеличения расстояния между сверхновой и Землёй. Наконец, третий вариант, это видимая, кажущаяся удалённость до точки вспышки в момент получения от неё света. Это весьма интересный вариант, поскольку он учитывает реальную скорость света, связанную с непрерывным расширением пространства. Пусть в момент получения света от сверхновой её реальная физическая удалённость возросла, например, в 2 раза по сравнению с исходной, в момент вспышки. Яркость этой вспышки будет видна на Земле такой, будто сверхновая находится немного ближе, чем эта реальная удалённость.

Самой большой удалённостью является вторая, поскольку за время света в пути пространство между звездой и Землёй все время возрастало. Третья удалённость учитывает время света в пути буквально , поэтому несколько условна, хотя и принимается, что видимая яркость галактики в точности соответствует её удалённости.

В пользу первого варианта удалённости сверхновой свидетельствует то, что фотоны, несущие информацию о ней, своеобразная фотография, удаляются от галактики сразу же после взрыва и становятся полностью независимыми от неё. Если, например, вспышка имеет синий цвет, а после неё, через какое-то время галактика становится красной или вообще гаснет, то на Земле будет получена именно "синяя" фотография. Именно этот поток фотонов и будет нести информацию об удалённости и скорости удаления галактики в момент вспышки . Это самая последняя информация о галактике на текущий момент времени, что особенно отчётливо видно, если галактика находится на горизонте видимости. В этом случае никакая новая информация о галактике после вспышки более не будет доступна.

Вместе с тем яркость вспышки непосредственно не является показателем удалённости галактики в момент её регистрации. Это связано с тем, что в процессе движения фотоны проходят путь меньший , чем окончательная дистанция между звездой и Землёй, в момент их регистрации. Собственно говоря, это довольно очевидно, поскольку в процессе их движения пространство непрерывно возрастает как между потоком фотонов и Землёй , так и между потоком и звездой . В результате и возникает это весьма интересное явление: фактический путь, пройденный фотоном от места вспышки до Земли, будет меньше , чем удалённость галактики от Земли в момент его регистрации. Яркость вспышки сверхновой определяется дистанцией, которую фотоны прошли реально . Эта дистанция, путь является фактически наблюдаемой удалённостью, поэтому на самом деле яркость вспышки с Земли будет видна несколько большей , чем она была бы в случае стационарной Вселенной.

Рассмотрим это явление подробнее. Для наглядности и упрощения вычислений вместо сверхновой и расширяющегося пространства Вселенной рассмотрим автомобиль, движущийся по непрерывно вытягивающейся трассе (рис.10.1). Пусть авто движется со скоростью v апо резиновой дорожке, которая растягивается, увеличиваясь за каждый фиксированный интервал времени Δt = t в е Htраз, где H – некоторая постоянная. В начальный момент времени авто находится на удалении S 0от конечной точки, от финиша. Условно принимаем, что движение авто и расширение дорожки происходят поочерёдно. Находим, что за первый интервал времени авто переместится от начальной точки на расстояние

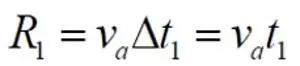
Пусть авто движется со скоростью v апо резиновой дорожке, которая растягивается, увеличиваясь за каждый фиксированный интервал времени Δt = t в е H tраз, где H – некоторая постоянная. В начальный момент времени авто находится на удалении S 0от конечной точки, от финиша.

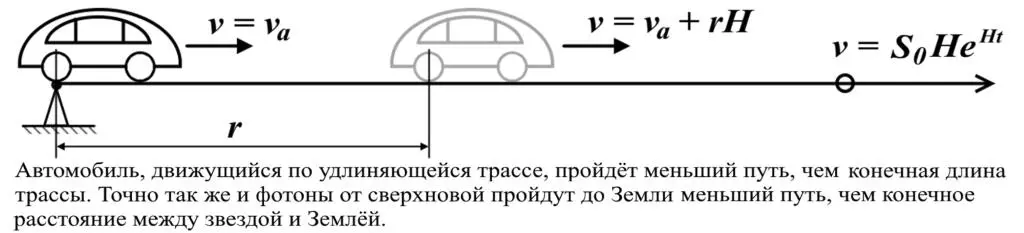
Рис.10.1

Условно принимаем, что движение авто и расширение дорожки происходят поочерёдно. Находим, что за первый интервал времени авто переместится от начальной точки на расстояние

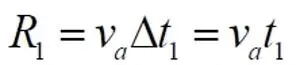
После этого отрезок R 0, путь, пройденный по дорожке, испытывает указанное расширение. Таким образом, за следующие два интервала времени удалённость авто от начальной точки увеличивается до нового значения

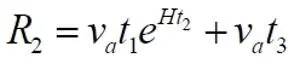
За четвёртый и пятый интервалы времени расстояние позади авто вновь возрастает, теперь уже до величины

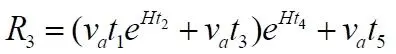
Далее этот новый формально пройденный интервал R 3, длина дорожки "позади" за следующую пару интервалов времени возросла до следующего нового значения

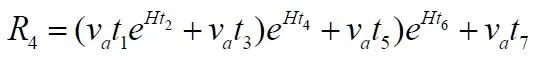
Здесь и в дальнейшем открывающие скобки в левой части уравнения мы не будем дублировать, чтобы не перегружать уравнение, просто помним, что число крайних левых скобок равно числу правых скобок.

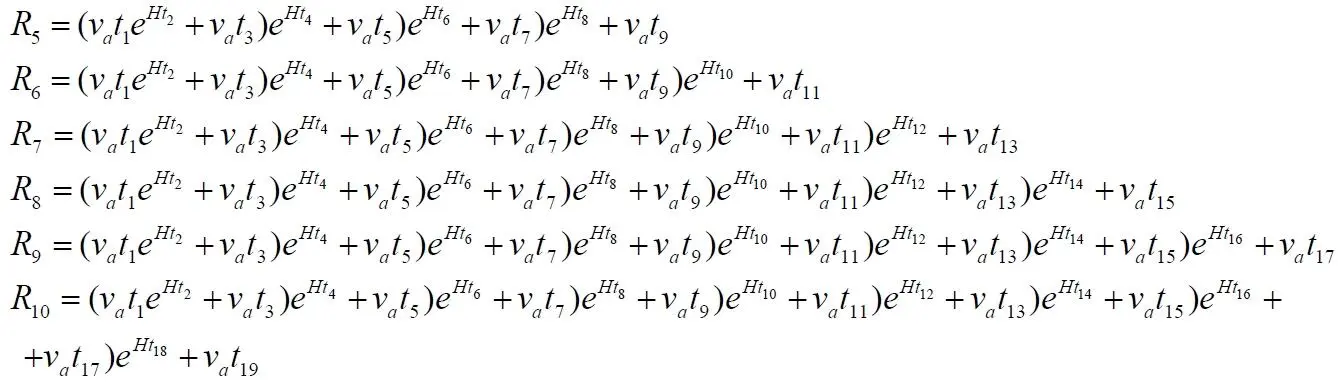
Для удобства, наглядности ограничимся на этом этапе десятью слагаемыми. Теперь для ещё большей наглядности уравнения последовательно раскроем скобки:

Число слагаемых, как мы и рассчитывали, равно 10, но число интервалов времени больше – 19. Понятно, что общее время движения T равно сумме всех интервалов Δt = t, поэтому можно записать T = (2n-1)t. Здесь мы учитываем, что все интервалы времени равны. Выносим общий множитель за скобки, а последнее слагаемое преобразуем в однотипную форму, добавив ему эквивалентный множитель, равный единице: