Александра Ведова - Геометрия. 7-9 класс
- Название:Геометрия. 7-9 класс
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:2020
- ISBN:978-5-532-07612-9
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Александра Ведова - Геометрия. 7-9 класс краткое содержание
Геометрия. 7-9 класс - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
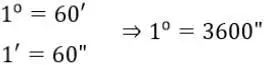
До 9 класса достаточно знать о градусах. О минутах и секундах рассказывают в 10 классе на уроках Алгебры, в разделе «Тригонометрия».
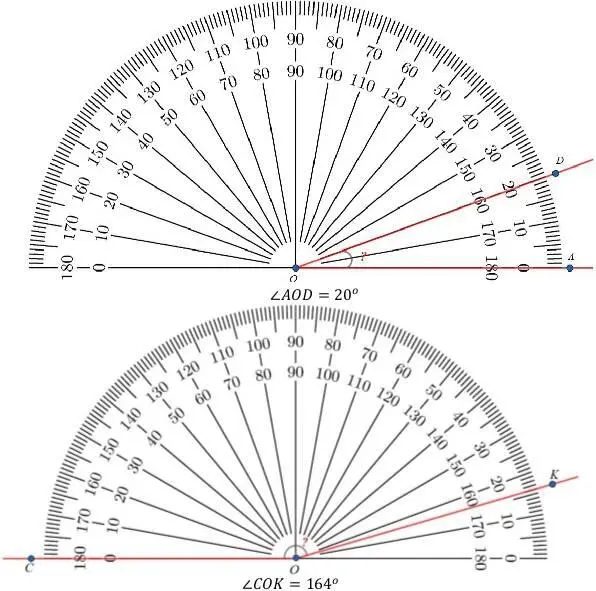
Измерить градусную меру угла можно транспортиром :
Общие сведения о треугольниках
Общие сведения, которые касаются всех треугольников:
1.Сумма углов в любом треугольнике равна ста восьмидесяти градусам
2.У любого треугольника есть средняя линия, длина которой равна половине основания.
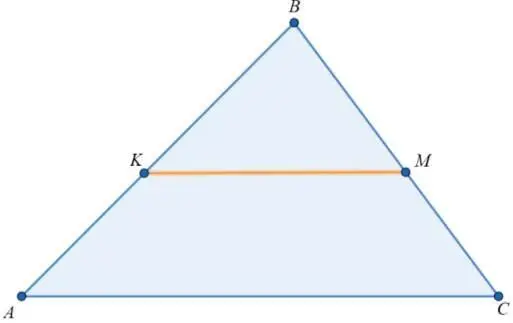
Средняя линия (K M) – это отрезок, который соединяет середины сторон, т.е. K – середина AB, M – середина BC.
Значит AK=KB, CM=BM
а 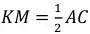 (основание для средней линии – это сторона, параллельная ей), т.е.
(основание для средней линии – это сторона, параллельная ей), т.е. 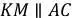
3.Кратчайшее расстояние от точки до прямой – перпендикуляр. Это понимание нужно для решений некоторых задач, где рисуя перпендикуляр то получается либо высота, либо прямоугольный треугольник , либо 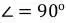

4.Площадь треугольника 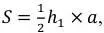 где a – основание (сторона, на которую опущена сторона),
где a – основание (сторона, на которую опущена сторона), 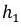 – это высота, опущенная на сторону а.
– это высота, опущенная на сторону а.
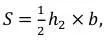
где b – это основание, а
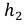
– это высота, опущенная на основание.
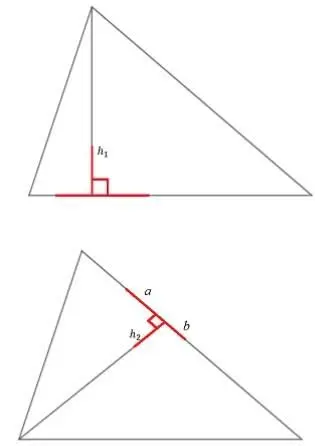
Т.е. площадь можно найти, используя половину произведения ЛЮБОЙ стороны и высоты, ОБЯЗАТЕЛЬНО опущенной именно на эту сторону.
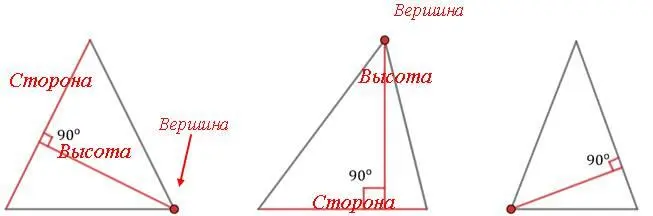
5.Высота – это отрезок, концы которого соединяют вершину треугольника и противоположную сторону так, что сторона и отрезок образуют 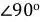 (прямой угол).
(прямой угол).
6.Медиана – это отрезок, соединяющий вершину треугольника и середину противоположной стороны. 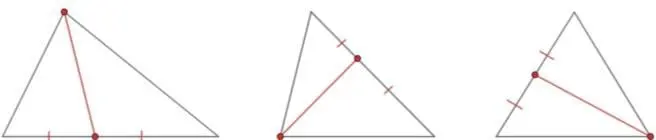
7.Биссектриса – это отрезок, исходящий из вершины на противоположную сторону и делящий угол пополам 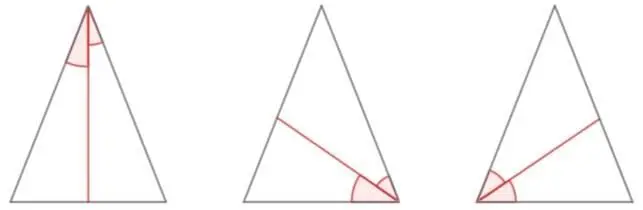 .
.
Виды и свойства треугольников.
Что такое треугольник, думаю, знают все: еще с начальной школы знаем, что такая фигура имеет три угла, три стороны и три вершины. Разберемся теперь, какие треугольники бывают.
В зависимости от углов:
остроугольные (все углы острые, меньше 90°)
тупоугольные (один из углов тупой, больше 90°)
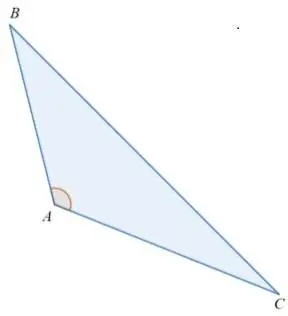
прямоугольные (один из углов прямой, 90°)

В зависимости от сторон:
произвольный (все стороны и углы разные)
равнобедренный (две стороны равны)
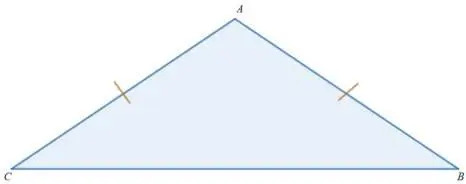
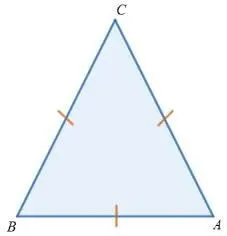
равносторонний (три стороны равны)
В планиметрии рассматривают: прямоугольные, равнобедренные и равносторонние треугольники – они немного особенные и свойств у них много, которые надо знать.
У остроугольного нет особенностей.
У тупоугольного есть одна: три высоты будут пересекаться вне треугольника.
Прямоугольный:
Стороны, прилежащие к углу в 90°, называются катетами
Сторона, лежащая напротив угла в 90°, называется гипотенузой
Свойства:
Два острых угла дают в сумме 90°. (Сумма углов в треугольнике составляет 180°, в прямоугольном – один угол прямой, т.е. 90°, 180°-90°=90°, таким образом на два острых угла приходится только 90°.)
Катет, лежащий напротив угла в 30°, равен половине гипотенузы.

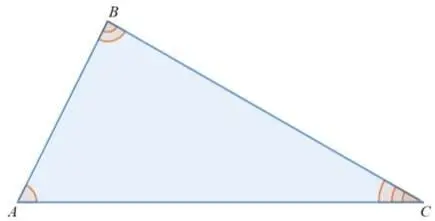
Равнобедренный:
Равные стороны называются боковыми, третья- основанием. Боковые стороны равны по определению.
Свойства:
Углы при основании равны.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.
Интервал:
Закладка:









