Игорь Казаринов - Геометрия простыми словами. 7-й класс. В помощь ученикам, учителям, репетиторам

© Игорь Владиславович Казаринов, 2022

ISBN 978-5-4493-6140-0

Создано в интеллектуальной издательской системе Ridero

Почему у многих учеников возникают проблемы с задачами по геометрии? Хочу немножко рассказать о теории – почему такое происходит, и что вы с этим можете сделать.

Обычно в школе уроки алгебры проходят почти каждый день.

Уроки геометрии – это обычно два-три раза в неделю. Что получается? Те понятия, которые изучаются на алгебре, ученики слышат каждый день. Каждый день они что-то говорят сами. Что-то говорит учитель. И эти слова хоть как-то остаются в голове.

Методы решения, которых в алгебре на самом деле не очень много, практикуют каждый день и ученики их усваивают как-то. Хотя многие ученики имеют при этом проблемы с алгеброй.

Но когда какой-то предмет рассматривается в течение 40 минут всего один или два раза в неделю (как это обстоит с геометрией), очень мало получается времени на то, чтобы ученик усвоил и понял самые основные моменты. И хотя, например, в алгебре – то, что сейчас изучается в школе – многие вещи были открыты всего четыреста лет назад. (Конечно, начала алгебры относятся к древним временам!) Но многие способы вычислений и формулы, которые сейчас практикуются, были открыты не так давно.

Теперь возьмём геометрию. «Геометрия», как в учебниках написано, это греческое слово, которое означает: «гео» – Земля, «метрос» – это мерить. То есть наука о измерении земли. Практически все данные (все теоремы и аксиомы) в учебнике геометрии были открыты и созданы, были разработаны древними греками две-три тысячи лет назад. Ничего нового с тех пор в школьной программе не появилось. Учебники геометрии практически не изменяются в течение очень многих лет. Это плюс!

Но… в чём же минус? Очень многие понятия в геометрии – они… не русские. То есть это слова такие как «катет», «гипотенуза», «тригонометрия», «медиана».

В геометрии учебники построены по принципу усложнения тем, но при решении более сложных задач часто надо очень уверенно применять знания самых простых первых правил и теорем.

Более того – обычно все сложные задачи сводятся к решению более простых, которые надо уметь заметить в сложной задаче. Поэтому без 100% уверенного понимания и умения применять данные из 7 класса не получится решить большинство задач по геометрии из старших классов и на итоговом экзамене по математике.

Помочь лучше разобраться и усвоить понятия геометрии поможет мой видео канал на Ютубе, который называется Igor Kazarinov. Его легко найти через любой поисковик в интернете, набрав мои имя и фамилию на русском «Игорь Казаринов». При этом вы также получите ссылки на мои сайты с различными статьями, касающимися обучения и ссылки на созданные мной группы в соцсетях – в Контакте.

На видеоканале можно найти плейлист «Геометрия»с роликами по геометрии.

Точкав геометрии – это место в пространстве, которое не имеет никаких измерений – ни длины, ни толщины, ни ширины. Совершенно ничего, вообще никаких измерений. Само понятие точки – это условность. Потому что в природе не существует ничего, что не имеет размера, даже атом имеет какие-то размеры, хотя и очень маленькие, и мы не можем его увидеть. Вторая условность – это то, как точка изображается. Точка в геометрии изображается маленьким кружочком. Точки в геометрии принято обозначать большими латинскими буквами. Например «точка А, точка В (бэ)». Латинские буквы – это алфавит который принят в геометрии, в математике и физике, в точных науках. Как ни странно – в учебниках геометрии определение точки не дается!

Ещё одно определение, которого нет в учебниках – это определение «прямой». Прямая рисуется тонкой линией, которая состоит из точек. Прямая – по словарю Ожегова – эта линия, подобная туго натянутой нити, которая продолжается до бесконечности в обе стороны. Можно сказать, что эта линия, которая идет до бесконечности в обе стороны и никуда на сворачивает. Эта линия состоит из точек и она тоже, как и точка, не имеет толщины. То есть это тоже условность, которая в природе не существует. Потому что никто не сможет назвать хоть что-то, что будет продолжаться в обе стороны до бесконечности и при этом никуда не будет сворачивать. То есть прямая – это условная линия, которую мы изучаем в геометрии, которая используется в геометрии, понятие, с помощью которого мы решаем какие-то задачи. Прямые обозначают двумя способами. Первый – это маленькая латинская буква, написанная рядом с линией прямой – например, «прямая a, прямая b».

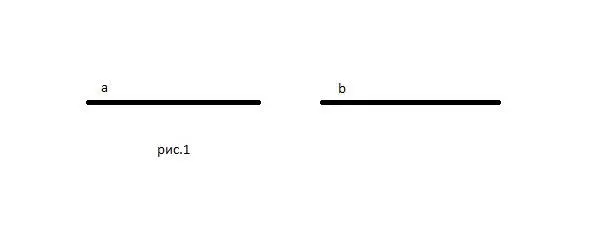
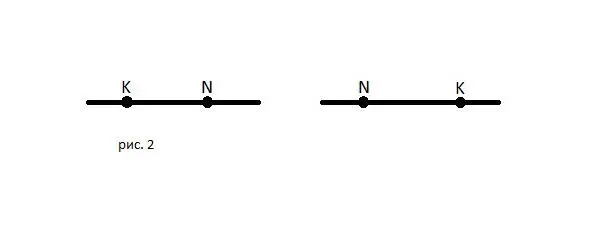
Также прямую можно обозначить по двум каким-то точкам, которые на ней находятся. Например, на прямой есть точка K и точка N. Тогда эту прямую можно назвать прямой KN. Также эту прямую можно узнать прямой NK, потому что нет никакой разницы – в каком направлении мы двигаемся по прямой. Прямая в обе стороны бесконечна. (рис.2)

Если я поставлю на этой же прямой третью точку – точку M, то я смогу также эту прямую назвать по двум любым точкам из трёх – прямой NM, прямой MK, прямой MN, или даже любые другие комбинации любых двух точек, принадлежащих этой прямой. (рис.3) По трём точкам прямая никогда не называется – то есть я не могу сказать, что это прямая MNK!

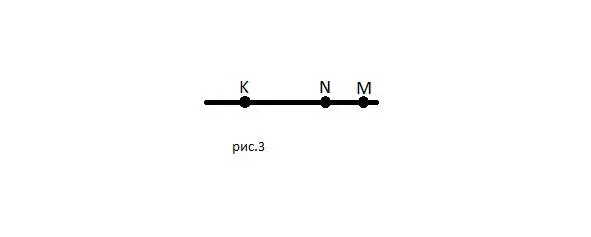
Прямая всегда называется только по двум точкам. Нужно иметь ввиду, что иногда в задачах учеников пытаются немножко запутать и одну и ту же прямую обозначают по-разному – двумя парами разных букв. Внимательно смотрите на задачи! Смотрите на чертеж и обращайте внимание на то – о какой прямой говорится в задаче, то есть – если там говорится, что есть «прямая MK», потом говорится что-то про «прямую а», то имейте ввиду, что это может быть одна и та же прямая, названная по-разному!

Прямые на плоскости могут пересекаться и могут не пересекаться. Прямые, которые не пересекаются называются параллельными (от греческих слов «пара» – рядом, «аллелон» – оба. То есть обе идут рядом друг с другом).