Яков Перельман - Живая математика. Занимательные задачи для любознательных умов

– Есть. Шестизначное число.

– Передайте бумажку соседу, что сидит подальше от меня. А он пусть разделит это шестизначное число на 7.

– Легко сказать: разделить на 7! Может, и не разделится.

– Не беспокойтесь, поделится без остатка.

– Числа не знаете, а уверены, что поделится.

– Сначала разделите, потом будем говорить.

– На ваше счастье, разделилось.

– Результат вручите своему соседу, не сообщая мне. Он разделит его на 11.

– Думаете, опять повезёт – разделится?

– Делите, остатка не получится.

– В самом деле без остатка! Теперь что?

– Передайте результат дальше. Разделим его… ну, скажем, на 13.

– Нехорошо выбрали. Без остатка на 13 мало чисел делится… Ан нет, разделилось нацело. Везёт же вам!

– Дайте мне бумажку с результатом; только сложите её, чтобы я не видел числа.

Не развёртывая листа бумаги, «фокусник» вручил его председателю.

– Извольте получить задуманное вами число. Правильно?

– Совершенно верно! – с удивлением ответил тот, взглянув на бумажку. – Именно это я и задумал… теперь, так как список ораторов исчерпан, позвольте закрыть наше собрание, благо и дождь успел пройти. Разгадки всех головоломок будут оглашены сегодня же, после ужина. Записки с решениями можете подавать мне.

1. Головоломка с белкой на поляне рассмотрена была полностью раньше. Переходим к следующей.

2.Нельзя считать, как многие делают, что 8 руб. уплачено за 8 поленьев, по 1 руб. за полено. Деньги эти уплачены только за третью часть от 8 поленьев, потому что огнём пользовались трое в одинаковой мере. Отсюда следует, что все 8 поленьев оценены были в 8 × 3, то есть в 24 руб., и цена одного полена – 3 руб.

Теперь легко сообразить, сколько причитается каждому. Пятёркиной за её 5 поленьев следует 15 руб.; но она сама воспользовалась плитой на 8 руб.; значит, ей остаётся дополучить ещё 15 – 8, то есть 7 руб. Тройкина за три своих полена должна получить 9 руб., а если вычесть 8 руб., причитающиеся с неё за пользование плитой, то следовать ей будет всего только 9–8, то есть 1 руб.

Итак, при правильном дележе Пятёркина должна получить 7 руб., Тройкина – 1 руб.

3. На первый вопрос – через сколько дней в школе соберутся одновременно все 5 кружков – мы легко ответим, если сумеем разыскать наименьшее из всех чисел, которое делится без остатка на 2, на 3, на 4, на 5 и на 6. Нетрудно сообразить, что число это 60. Значит, на 61-й день соберутся снова 5 кружков: политический – через 30 двухдневных промежутков, военный – через 20 трёхдневных, фотокружок – через 15 четырёхдневных, шахматный – через 12 пятидневок и хоровой – через 10 шестидневок. Раньше чем через 60 дней такого вечера не будет. Следующий подобный же вечер будет ещё через 60 дней, то есть уже во втором квартале.

Итак, в течение первого квартала окажется только один вечер, когда в клубе снова соберутся для занятий все 5 кружков.

Хлопотливее найти ответ на второй вопрос задачи: сколько будет вечеров, свободных от кружковых занятий? Чтобы разыскать такие дни, надо выписать по порядку все числа от 1 до 90 и зачеркнуть в этом ряду дни работы политкружка, то есть числа 1, 3, 5, 7, 9 и т. д. Потом зачеркнуть дни работы военного кружка: 4-й, 10-й и т. д. После того как зачеркнём затем дни занятий фотокружка, шахматного и хорового, у нас останутся незачёркнутыми те дни первого квартала, когда ни один кружок не работал.

Кто проделает эту работу, тот убедится, что вечеров, свободных от занятий, в течение первого квартала будет довольно много: 24. В январе их 8, а именно: 2-го, 8-го, 12-го, 14-го, 18-го, 20-го, 24-го и 30-го. В феврале насчитывается 7 таких дней, в марте – 9.

4.Оба насчитали одинаковое число прохожих. Хотя тот, кто стоял у ворот, считал проходивших в обе стороны, зато тот, кто ходил, видел вдвое больше встречных людей.

5.С первого взгляда может действительно показаться, что задача неправильно составлена: выходит как будто, что внук и дед одного возраста. Однако требование задачи, как сейчас увидим, легко удовлетворяется.

Внук, очевидно, родился в XX столетии. Первые две цифры года его рождения, следовательно, 19: таково число сотен. Число, выражаемое остальными цифрами, будучи сложено с самим собою, должно составить 32. Значит, это число 16: год рождения внука 1916, и ему в 1932 году было 16 лет.

Дед его родился, конечно, в XIX столетии; первые две цифры года его рождения 18. Удвоенное число, выражаемое остальными цифрами, должно составить 132. Значит, само это число равно половине 132, то есть 66. Дед родился в 1866 году, и ему в 1932 году было 66 лет.

Таким образом, и внуку, и деду в 1932 году было столько лет, сколько выражают последние две цифры годов их рождения.

6.На каждой из 25 станций пассажиры могут требовать билет до любой станции, то есть на 24 пункта. Значит, разных билетов надо напечатать 25 × 24 = 600 образцов.

7. Задача эта никакого противоречия не содержит. Не следует думать, что дирижабль летел по контуру квадрата: надо принять в расчёт шарообразную форму Земли. Дело в том, что меридианы к северу сближаются (рис. 6); поэтому, пройдя 500 км по параллельному кругу, расположенному на 500 км севернее широты Ленинграда, дирижабль отошёл к востоку на большее число градусов , чем пролетел потом в обратном направлении, очутившись снова на широте Ленинграда. В результате дирижабль, закончив полёт, оказался восточнее Ленинграда.

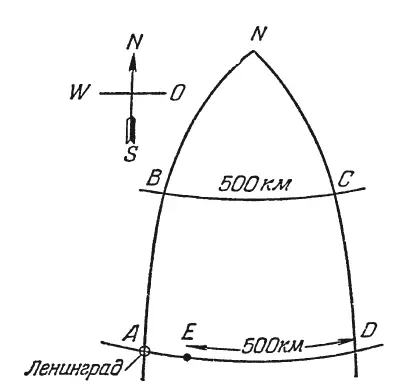
Рис. 6

На сколько именно? Это можно рассчитать. На рис. 6 вы видите маршрут дирижабля: АВСВЕ. Точка N —

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.