Владимир Левшин - Новые рассказы Рассеянного Магистра

— Не беда! — нашёлся Нулик. — При мне всегда запасной колокольчик.

Он схватил на руки Пончика, пощекотал его под подбородком — тот несколько раз тявкнул.

— Объявляю заседание открытым, — невозмутимо провозгласил Нулик. — Чур, первый вопрос мой. Прошу разъяснить: могут ли рыбы смеяться и что смешного в геометрии?

Сева удивлённо поднял брови.

— Мне кажется, вопрос уважаемого президента к делу не относится.

— То есть как это не относится? — возмутился Нулик — Магистр пишет, что смеялся каким-то сардиническим и даже геометрическим смехом. Но разве сардинки умеют смеяться?

Не знаю, как сардинки, а мы посмеялись вволю. Президент, как водится, поначалу обиделся, но потом не выдержал и стал хохотать заодно со всеми.

— Да будет тебе известно, — выговорил наконец Сева, — что сардинического смеха в природе не существует Есть сардонический.

Нулик пожал плечами.

— Сардонический? Это уж совсем непонятно.

— Почитай энциклопедию — поймёшь! — посоветовала Таня.

— Сама читай! — огрызнулся Нулик.

— А я уж прочитала.

— И что же вычитала?

— А то, что сардоническим называется смех язвительный, насмешливый, горький. И связано это с ядовитой травой сардонией. Если её поесть, лицо начинает дёргаться, кривиться.

— Так? — спросил президент и принялся корчить какие-то немыслимые рожи.

Сева безнадёжно махнул рукой.

— Ну, выпустила джинна из бутылки! Теперь конца не жди…

Действительно, президент так обрадовался возможности подурачиться, что, казалось, начисто позабыл о своём высоком сане и о научно-исследовательских интересах клуба. Но Олег сумел-таки призвать его к порядку.

— Между прочим, — сказал он, — Магистр не так уж сильно ошибся, когда назвал смех сардиническим. Ведь трава сардония растёт на острове Сардиния… От него, кстати, и получила название та вкусная рыбка, которая ловится в тех местах.

— Вот видите! — торжествовал Нулик. — Я всегда говорил, что Магистр — умница. У него даже и ошибки умные. Наверное, и «геометрический смех» не такая уж глупость.

— К сожалению, не могу с тобой согласиться, — сказал Олег. — Магистр, конечно же, имел ввиду гомерический смех, который никакого отношения к геометрии не имеет.

— А к чему, позвольте узнать, он имеет отношение?

— К Гомеру. Великому поэту Древней Эллады. Автору бессмертных поэм «Илиада» и «Одиссея».

Нулик досадливо топнул ножкой.

— Но при чём же тут гомерический смех?

— А при том, что в «Илиаде» есть одна сцена, где живущие на горе Олимп боги громоподобно хохочут над своим собратом Геф е стом.

— А чем он их насмешил?

— Бог огня и покровитель кузнецов Гефест был хромой и некрасивый. Наблюдая, как он хлопочет, готовя для них угощение, боги хохотали над его неуклюжими движениями.

— «Смех несказанный воздвигли блаженные жители неба, видя, как с кубком Гефест по чертогу вокруг суетится», — торжественно продекламировал Сева.

— Садитесь. Ставлю вам пять. — изрёк Олег профессорским тоном. — Надеюсь, теперь понятно, какой смех называют гомерическим.

— Моя мама говорит, что над физическими недостатками смеются только нравственные уроды, — сказал Нулик непривычно жёстко.

От неожиданности Сева даже присвистнул.

— Это ты верно говоришь! Олимпийские боги и впрямь особой добротой не отличались Это ведь они приковали к скале Промет е я за то, что он похитил божественный огонь и отдал его людям.

— А что они сделали с Сизифом? — напомнила Таня. — Он хотел избавить людей от смерти, а его за это отправили в ад и заставили там вечно вкатывать на гору огромный камень

— Стоп! — вмешался я. — На этот раз достаточно. Олимпийские боги совершили столько жестокостей, что перечисление их отняло бы слишком много времени. Займёмся лучше Единичкой. Как удалось ей так быстро перемножить в уме два многозначных числа, а потом, прибавив к произведению единицу, извлечь из этого квадратный корень?

— По-моему, ничего она не перемножала и не извлекала, — сказала Таня. — Просто применила какой-то способ.

Нулик стукнул себя кулачком в грудь.

— Спроси об этом у меня.

— Вот чудо! — всполошились все. — Ты знаешь Единичкин способ?

— Знать-то знаю, но… — Нулик почесал в затылке.

— Что ещё?

— Но применим ли он во всех случаях жизни? Вот вопрос…

— Об этом после, а пока давай рассказывай.

Нулик откашлялся.

— Леди и джентльмены, прошу внимания. Возьмём два последовательных нечётных числа: например, 15 и 17. Насколько я понимаю в арифметике, произведение их равно 255. Так? Теперь прибавим единицу. Что мы имеем? 256 Извлечём из 256 квадратный корень. Это всегда было и будет 16. А теперь сравните-ка ответ с заданными числами: 15 и 17. Что вы замечаете? Вы замечаете, что 16 есть среднее арифметическое между 15 и 17, то есть число, которое заключено между ними.

— Гениально! Я бы до такого нипочём не додумался! — уверял Сева.

Нулик сиял как медный грош, но скромность и преданность научным интересам заставили его снова обратиться к слабой стороне своего научного открытия.

— Хотел бы я знать, годится ли способ Единички для десяти- или двадцатизначных чисел?

— Так это же легко проверить, — сказал Олег.

— Что ты! — испугался Нулик. — Перемножать в уме такие огромные числа!

— Зачем перемножать? Просто решим задачу в общем виде. Обозначим первое из двух нечётных чисел буквой а. Тогда второе число будет а + 2 — ведь каждое следующее нечётное число больше предыдущего на 2. Теперь перемножим эти числа. Получим а ( а + 2). Затем прибавим к этому 1. Получим а ( а + 2) + 1. И, наконец, извлечём из всего этого квадратный корень

Вот и всё, — закончил Олег. — Вернее, почти всё.

— Очень даже почти! — подтвердил Нулик.

— Нет, не очень! Ведь подкоренное выражение а ( а + 2) + 1 можно преобразовать так: а 2+ 2 а + 1 А этот трёхчлен не что иное, как полный квадрат суммы, то есть ( а + 1) 2. А уж извлечь квадратный корень из квадрата проще пареной репы:

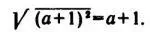
Вот теперь совсем всё!

— Теперь совсем! — согласился Нулик. — Потому что а + 1 это и есть число, стоящее между а и а +2, то есть их среднее арифметическое. Стало быть, способ годится для всех чисел.

На радостях президент прошёлся колесом по комнате, потом схватил на руки Пончика и принялся танцевать с ним вальс. Он веселился так бурно, что пришлось объявить антракт.

— А в антракте полагается идти в буфет! — заявил Нулик и с азартом набросился на бутерброды, приготовленные Таней.