Льюис Кэрролл - История с узелками

10 картин получают 29 оценок, распределенных следующим образом:

Расставив все крестики и заключив в скобки те из них, которые по условиям задачи необязательны, мы получим 10 картин, оценки которых распределены так:

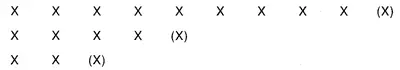
Расставив все нули, но не от начала к концу, как крестики, а в обратном направлении — от конца к началу, мы получим 9 картин с оценками, распределенными так:

Единственное, что еще необходимо сделать после этого, — вдвинуть оба клина как можно плотнее друг в друга, чтобы число отмеченных картин было минимальным. Если та или иная необязательная оценка мешает нам загонять клин в клин, мы ее стираем, если же не мешает — оставляем в целости и сохранности. В первом и третьем рядах оказывается по 10 обязательных оценок, а в середине — лишь 7. Следовательно, необходимо стереть все необязательные оценки в первом и третьем рядах обоих клиньев и оставить все необязательные оценки, стоящие в середине.

В начале года у каждого из братьев Аи Вбыло по 1000 фунтов стерлингов. Через год братья в своем письме губернатору Кговджни уведомляют его, что в день отправления письма они, как никогда, близки к 60 000 фунтов стерлингов. Каким образом им это удалось?

В день отправления письма братья впервые решили прогуляться близ Английского банка, в подвалах которого хранилась указанная сумма.

На эту задачу было получено два в высшей степени замечательных ответа. Читатель, у которого Сумбур в голове (это его псевдоним), заставил братьев занять 0 пенсов и украсть 0 пенсов, а затем приписать обе «добытые» цифры справа от 1000 фунтов. В результате столь невинной операции у братьев оказывается 100 000 фунтов, что значительно превышает те 60 000, о которых идет речь в задаче. At Spes Infracta [6]нашел еще более остроумное решение: пользуясь взятым взаймы нулем, этот читатель превращает 1, с которой начинается 1000 фунтов одного брата, в 9, прибавляет «добычу» к исходной 1000 фунтов другого брата, получая в результате 10 000 фунтов. С помощью «украденного» нуля At Spes Infracta превращает 1 в 6 и тем самым достигает требуемой в условии задачи суммы в 60 000 фунтов.

Лоло ( Л) успевает связать 5 шарфов за то время, пока Мими ( М) вяжет 2. Зузу ( З) успевает связать 4 шарфа за то время, пока Лоло вяжет 3. Пять шарфов Зузу весят столько же, сколько один шарф Лоло. Пять шарфов Мими весят столько же, сколько 3 шарфа Зузу. Один шарф Мими греет так же, как 4 шарфа Зузу а один шарф Лоло — как 3 шарфа Мими. Какая из трех вязальщиц лучше, если быстроту вязки, легкость шарфа и его способность сохранять тепло оценивать одинаково?

Места на конкурсе вязальщиц шарфов распределились следующим образом: 1) М, 2) Л, 3) З.

При прочих равных условиях Лпревосходит Мпо быстроте вязки в 5/ 2раза, а Зпревосходит Лв 4/ 3раза. Чтобы найти 3 числа, удовлетворяющих этим условиям, проще всего принять скорость, с которой вяжет Л(ибо Лнепосредственно связана и с М, и с З), за 1, а скорость, с которой вяжут ее конкурентки, выразить в виде дробей. В этих единицах качество работы Л, Ми Зоценивается числами 1, 2/ 3и 4/ 3.

Для оценки легкости шарфа следует иметь в виду, что, чем больше вес, тем менее искусной следует считать вязальщицу. Следовательно, качество шарфов Зотносится к качеству шарфов Л, как 5 к 1. Таким образом, при оценке легкости шарфов Л, Ми Зполучают оценки 1/ 5, 5/ 3и 1. Аналогичным образом оценивается и умение Л, Ми Звязать теплые шарфы: 3, 1 и 1/ 4. Чтобы получить окончательный результат, необходимо перемножить три оценки, полученные Л, и проделать ту же операцию с оценками Ми З. В итоге мы получим: 1× 1/ 5×3, 2/ 5× 5/ 3×1, 4/ 3×1× 1/ 4то есть 3/ 5, 2/ 3и 1/ 3. Умножив все три числа на 15 (отчего отношение любых из них не изменится), мы получим оценки 9, 10 и 5. Следовательно, лучшей вязальщицей необходимо признать М, затем идет Ли, наконец, З.

Почему оценки претенденток надлежит именно перемножать, а не складывать, подробно объясняется, во многих учебниках, и я не буду занимать здесь место повторением избитых истин. Однако проиллюстрировать необходимость умножения можно очень легко на примере длины, ширины и глубины. Представим себе, что два землекопа Аи Впожелали узнать, кто из них более искусен в своем ремесле. Оба копают ямы в форме прямоугольного параллелепипеда. Количество проделанной работы измеряется числом кубических футов вынутой земли. Предположим, что Авыкопал яму длиной 10, шириной 10 и глубиной 2 фута, а Ввыкопал яму длиной 6, шириной 5 и глубиной 10 футов. Объем первой ямы равен 200, а второй — 300 кубическим футам. Следовательно, Bсправляется со своим делом в 3/ 2раза лучше, чем А. А теперь попробуйте оценить по десятибалльной системе длину, ширину и глубину каждой из ям, а затем сложить оценки. Что у вас получится?

Некоторые письма, полученные в связи с узелком VI, навели меня на мысль о желательности дополнительных объяснений.

Первая задача, разумеется, не более чем шутка, основанная на игре слов. Я считал, что подобная вольность вполне допустима в серии задач, призванной не столько поучать, сколько развлекать. Однако двое моих корреспондентов, полагающих, что Аполлон должен всегда быть начеку и не ослаблять тетивы своего разящего лука, обрушились на задачку о 60 000 фунтов стерлингов с уничтожающей критикой. Кстати сказать, ни один из них не смог решить задачу, но такова уж человеческая натура.

Как-то раз (для желающих я могу назвать точную дату: 31 сентября) я встретил своего старого друга Брауна и загадал ему только что услышанную загадку. Мощным усилием своего колоссального интеллекта Браун разгадал ее. «Правильно!» — сказал я, услышав ответ. «Очень хорошая загадка, — похвалил меня Браун, — не всякий ее разгадает. Нет, что и говорить, загадка — просто прелесть!» Не успел я распрощаться с Брауном, как через несколько шагов налетел на Смита и задал ему ту же загадку. Тот на минуту наморщил лоб, а потом махнул рукой. Дрожащим голосом я робко пролепетал ответ. «Дурацкая загадка, сэр! — недовольно проворчал Смит на прощание. — Глупее не придумаешь! Удивляюсь, как вы решаетесь повторять подобную чепуху!» Тем не менее есть все основания считать, что Смит по уму не только не уступает Брауну, но и, быть может, даже превосходит его!