Владимир Карцев - Приключения великих уравнений

Максвеллу нравится, что Фарадей признает рациональное зерно, имеющееся в работах чуждых ему по духу и манере исследователей, например Ампера. Так, он принимает целиком идею кругового магнитного поля, окружающего провод с электрическим током.

Максвеллу эта идея кажется правильной. Более того, тезис «каждый электрический ток окружен магнитным полем» легко ложится в рамки сравнительно несложных математических символов и операций. «Легкость» и «несложность», конечно, весьма относительные. Максвелл отдал своей теории электромагнитного поля полжизни.

Математические формулы, о которых идет речь, изучаются современными студентами в курсах высшей математики и теоретической электротехники лишь в последние годы занятий в вузах. Однако гений Максвелла был «легким» — все, знавшие его, не уставали повторять, что он делал свои открытия как бы играя. Такому впечатлению способствовала и манера Максвелла заходить в лабораторию вроде бы между прочим, по пути, проходя мимо, иной раз с собакой.

* * *

Режим Максвелла непостижим: он спал с пяти до половины десятого вечера. Затем — занятия до двух ночи. С двух до половины третьего — гимнастика: беготня по лестницам и коридорам преподавательского общежития (можно представить себе силу возмущения общественности — впрочем, тогда стены делали толще). Затем — сон до семи утра. С семи утра — новый рабочий день.

* * *

Эта манера, повторенная в сотнях экземпляров другими английскими физиками, подражавшими Максвеллу, если читатель помнит, юмористически описана в сборнике «Физики шутят», выпущенном издательством «Мир».

Итак, и Ампер, и Фарадей считали, что каждый электрический ток окружен магнитным полем. Максвелл решает записать этот тезис в форме уравнения

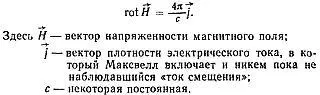
Смысл этого выражения может быть понят относительно легко даже неспециалистом.

Обозначение rot — сокращение от слова roto r — вихрь.

(Максвелл использовал слово curl — завиток); операция rot , грубо говоря, показывает в данном случае, что вектор напряженности магнитного поля вращается вокруг вектора тока плотностью j.

Другой, сразу завоевавшей признание Максвелла идеей стало представление Фарадея о природе электромагнитной индукции — то есть возникновение электричества в контуре, число магнитных силовых линий в котором изменяется то ли вследствие относительного движения контура и магнита, то ли вследствие изменения магнитного поля.

* * *

Максвелл, рассказывают, обладал способностью читать лекцию для трех человек с тем же воодушевлением и подъемом, что и перед огромной аудиторией.

Максвелл писал (и изредка публиковал под псевдонимом dp/dt ) стихи. Большое место в его поэтическом творчестве занимают сатирические стихотворения: «Доказательство нецелесообразности чтения лекций в ноябре», «Проблемы динамики» (юмористическое решение дифференциального уравнения), «Лекция по физике для молодых женщин» (место действия — уютная комнатка, тема лекции — зеркальный гальванометр Томсона, аудитория — один человек), «Кошачья колыбельная», «Парадоксальная ода», посвященная автору книги «Парадоксальная философия».

* * *

Эта зависимость также вполне укладывалась во внешне формальные математические операции. После многолетних трудов Максвелл записал строку:

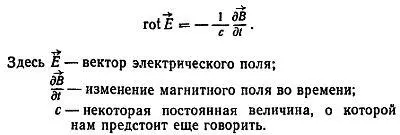
Формула настолько физически прозрачна, что ей тоже можно, при известном упрощении, придать ясный смысл.

Операция означает, грубо говоря, вращение вектора E -> , охват им некоторого источника, которым в данном случае является изменение магнитного поля В -> .

В контуре, охватывающем источник изменяющегося магнитного поля, наведется электродвижущая сила, а в пространстве возникнет новое электрическое поле. Что означает минус перед правой частью уравнения? Он тоже вполне физически обоснован — на основании закона, открытого русским физиком Э. X. Ленцем, направление тока, возникающего в замкнутом контуре в результате электромагнитной индукции, таково, что ток препятствует изменению магнитного потока (инерция магнитного поля).

Но необходимо учесть еще одно важное свойство торов электрической и магнитной индукций Е -> и В -> , представляющих собой математическое обозначение электрических и магнитных силовых линий: в то время как электрические силовые линии начинаются и кончаются на зарядах, являющихся источниками поля, магнитные силовые линии располагаются кольцеобразно: а у кольца, как известно, «нет ни начала, ни конца», следовательно, силовые линии магнитного поля не могут где-то начинаться, где-то кончаться — они замкнуты сами на себя.

В математике для обозначения ситуации с источниками поля можно применить операцию «дивергенция» (Максвелл использовал слово «конвергенция»).

Дивергенция — мера источника. Например, свеча — источник света — обладает положительной дивергенцией, ночной мрак за окном, где свет рассеивается, поглощается, обладает дивергенцией отрицательной. Что касается оконного стекла, где число «лучей», пришедших из комнаты, равно числу лучей, ушедших в темноту, то там дивергенция равна нулю. В стекле свет не создается, не поглощается (если оно, разумеется, достаточно прозрачное).

Поэтому Максвелл добавляет к двум имеющимся уравнениям еще два:

Физический смысл уравнений прозрачен.

Силовые линии электрического поля кончаются на зарядах, плотность которых р .

Силовые линии магнитного поля не кончаются нигде — они замкнуты сами на себя.

Вот какая система уравнений появилась в результате работ Максвелла:

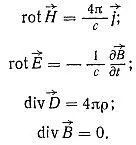
Входящие в эти уравнения векторы электрической и магнитной индукции ( D -> и В -> ) и векторы напряжснностей электрического и магнитного полей ( Е -> и H -> ) связаны стыми соотношениями: D -> = εЕ -> и В -> = μН -> ,

где μ — магнитная проницаемость среды,

ε — диэлектрическая постоянная среды.

Четыре строчки этих простых уравнений и составляют «уравнения Максвелла», а система взглядов, которая легла в основу уравнений, получила название «максвелловой теории электромагнитного поля».

Уравнения были просты, но чем больше Максвелл и его последователи над ними работали, тем больший внутренний смысл находили в четырех строчках. Генрих 160 Герц, знаменитый немецкий физик, роль которого в истории— доказать полную справедливость представлений Максвелла, писал о неисчерпаемости теории Максвелла: