Сэм Лойд - Самые знаменитые головоломки мира

Сколько суток пройдет в Капитолии с момента, когда орел улетел, до момента, когда он, облетев земной шар в западном направлении по кругу, вновь сядет на прежнее место?

Вы видите на рисунке, как король Страны Головоломок и принцесса Загадка исследуют тайны знаменитой печати царя Соломона, изображенной на его гробнице. Король пытается подсчитать, сколько на этом рисунке можно обнаружить различных равносторонних треугольников. А как полагаете вы?

Юный заяц-спортсмен и черепаха бегут в противоположных направлениях по круговой дорожке, диаметр которой 100 ярдов. Они начали свой забег в одном и том же месте, но заяц не бежал до тех пор, пока черепаха не прошла 1/ 8часть всей дистанции (то есть окружности данного круга). Заяц придерживается столь невысокого мнения о спортивных качествах своей соперницы, что он лениво бежит, пощипывая травку, до тех пор, пока не встречается с черепахой. К этому времени он проходит 1/ 6всей дистанции. Во сколько раз быстрее, чем до сих пор, придется теперь бежать зайцу, чтобы он выиграл этот забег?

Эта хорошенькая швейцарка очень искусна в решении геометрических головоломок на разрезание. Она сумела найти способ, с помощью которого кусок красных обоев, что находится в ее правой руке, можно разрезать на две части, чтобы сложить из них швейцарский флаг. Вы видите его в левой руке девушки, белый крест в центре флага образует дыра. Разрез должен идти вдоль прямых, указанных на обоях.

Кроме того, швейцарка просит вас разрезать флаг, который она держит в левой руке, на две части, из которых можно было бы сложить прямоугольник размером 5x6.

Однажды я повстречал электрика, который сделал что-то вроде распределительного щита и хотел определить наиболее экономный способ протянуть хороший дорогой провод через все его контакты. Щит содержал несколько сот контактов, но я хочу познакомить читателей с самой идеей их соединения, а потому ограничусь участком 8x8, содержащим 64 контакта, который и показан на рисунке.

Задача состоит в том, чтобы определить кратчайшую длину провода, который должен из точки В протянуться в центр маленького квадратика, обозначенного буквой А, через центры всех 64 маленьких квадратиков. Сторона каждого квадратика равна 1 дюйму, а расстояние между центрами двух соседних квадратиков равно 3 дюймам. Каждый раз при изменении направления провод необходимо обернуть вокруг угла квадратика; на эту операцию уходит 2 дюйма провода. Никакие соединения по диагонали не допускаются.

Предположим, что для соединения точки В с центром ближайшего квадратика расходуется 2 дюйма провода. Можете ли вы определить наикратчайшую длину провода, необходимого для того, чтобы соединить В с A?

В старой задаче, которую можно найти во многих сборниках головоломок, речь идет об армейской колонне длиной в 50 миль. Пока колонна движется вперед с постоянной скоростью, курьер скачет из арьергарда в авангард, чтобы передать пакет, а затем возвращается обратно. Назад он прибывает как раз в тот момент, когда колонна прошла 50 миль. Какое расстояние проделал курьер?

Если бы колонна стояла на месте, то, очевидно, он бы проделал 50 миль туда и 50 миль, обратно. Но поскольку она движется вперед, всадник должен проделать более 50 миль, пока доберется до головы колонны, а возвращаясь назад, он проедет меньше 50 миль, ибо колонна движется ему навстречу. Предполагается, конечно, что скорость курьера постоянна.

Более трудная разновидность этой головоломки состоит в следующем. Армия, построившись вкаре 50 х 50 миль, проходит 50 миль вперед. Курьер, выехав из середины заднего ряда, пока армия движется вперед, объезжает вокруг всего каре и возвращается в исходную точку. Какое расстояние проезжает курьер?

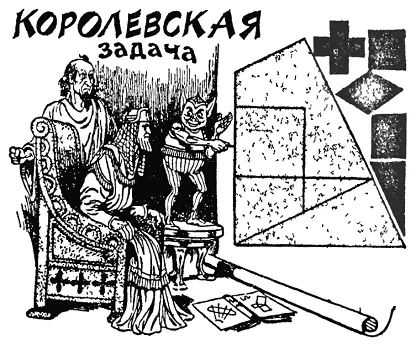
Беппо, королевский шут, объясняет Птолемею, как разрезать фигуру, напоминающую трапецию, на 5 частей, которые можно использовать в шести восхитительных головоломках. Нарисуйте такую фигуру на куске картона, разрежьте ее на 5 частей, а затем попытайтесь из них сложить:

1) квадрат,

2) греческий крест;

3) ромб;

4) прямоугольник;

5) прямоугольный треугольник;

6) исходную трапециевидную фигуру. Первые 5 фигур показаны на рисунке справа. При складывании каждой из шести фигур должны быть использованы все 5 частей.

Миссис Хуббард придумала оригинальную систему хранения банок с ежевичным джемом. Она расположила их в своем буфете таким образом, что на каждой полке находится по 20 кварт джема. Банки же в ее хозяйстве трех размеров. Можете ли вы сказать, сколько кварт содержится в банке каждого размера?

Электрика пригласили провести звонок в зале для собраний. Звонок должен быть в середине стены за президиумом, а кнопка его – у входной двери, дабы удобнее было напоминать разболтавшимся ораторам, что пора заканчивать выступление. Длина провода, необходимого для такой проводки, породила жаркую дискуссию, к которой привлекли и меня.

Зал, как показано на рисунке, имел в длину 30, а в ширину и высоту – 12 футов. Провод должен идти от звонка, который расположен в 3 футах от потолка в середине дальней стены, к кнопке, расположенной в 3 футах от пола в середине ближней стены. Провод может проходить по стенам, полу и потолку. Задача состоит в том, чтобы определить наикратчайший путь, по которому можно проложить провод. Толщиной стен и кнопки следует пренебречь.