Сэм Лойд - Самые знаменитые головоломки мира

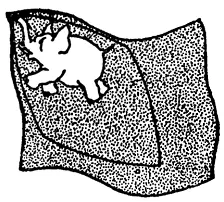
Наикратчайший путь на плане сада такой: 15, 16, 12, 11, 10, 14, 13, 9, 5, 1, 2, 6, 7, 8, 4, 3, «сердечко».

217. [Пусть х – число акров, а у – число бушелей, тогда можно составить следующие уравнения:

(3/4у + 80)/ x = 7,

(y + 80)/x = 8

Решая их, мы находим, что фермер отдавал ежегодно в уплату за аренду 80 бушелей, а на его ферме было 20 акров земли. – М. Г.]

218. [Если х – вес (в фунтах) индюков, купленных миссис О'Флаерти, равный по условию весу гусей, то можно составить уравнение

21x/24 + 21x/18 = 2x + 2

Отсюда х = 18. Следовательно, миссис О'Флаерти потратила 11,52 доллара на индюков и 8,64 доллара на гусей, то есть общая сумма затрат составила 20,16 доллара. – M Г. ]

219. Костюм был продан за 13,75 доллара.

220. Джимми 10лет и 16/21 года.

221. [Сам С. Лойд не объясняет выигрышной стратегии этой игры. Стратегия фермера состоит в том, чтобы ходить в диагонально противоположные углы квадратов до тех пор, пока он не загонит индюка к краю доски, после чего он уже легко может выиграть. Если фермер ходит первым, он должен ходить на ячейку 35. Индюк не может добиться преимущества, поскольку место между ячейками 9 и 10 пусто. Следующая типичная игра прояснит стратегию:

– М. Г.]

Вторая головоломка решается в 24 хода следующим образом: 52, 14, 15, 8, 9, 16, 18, 10, 11, 42, 39, 31, 33, 25, 22, 45, 50, 4, 5, 64, 60, 2, 3, 7.

222. На рисунке видно, что ювелир украл из каждого горизонтального ряда по камню, а затем переставил нижний камень на самый верх.

223. [Практически это разновидность задачи 194. Приложив треугольник к квадрату, как показано на первом рисунке к решению задачи 194, данную задачу можно решить с пятью частями. Поскольку в данной задаче треугольник составляет меньшую часть квадрата, чем в задаче 194, другие два способа решения последней здесь неприложимы. – M. Г. ]

224. Миссис О'Нейл потратила на бананы 33,6 доллара. На эти деньги она могла купить по 48 гроздей красных и желтых бананов, а всего – 96 гроздей. Но поделив всю сумму пополам и затратив 16,8 доллара на красные и 16,8 доллара на желтые бананы, она могла бы купить 42 грозди красных и 56 гроздей желтых бананов, то есть всего 98 гроздей.

225. Джоко движется от окна к окну в следующем порядке: 10, 11, 12, 8, 4, 3, 7, 6, 2, 1, 5, 9. Этот путь проходит по широкому пространству между нижним и средним рядами окон только дважды.

226. Головоломку можно решить за 8 ходов следующим образом: Тафт перепрыгивает последовательно через Нокса, Джонсона, Лаффолета и Кэннона. Грей перепрыгивает через Фербенкса. Хьюг перепрыгивает через Брайена. Грей перепрыгивает через Хьюга. Тафт перепрыгивает через Грея.

[Если мы будем рассматривать серию последовательных прыжков одного человека как один ход, то в решении Лойда требуется 5 ходов. Однако задачу можно решить всего за 4 хода. – M Г.]

227. Ответ ясен из рисунка.

228. Кость должна выпасть единицей вверх. Если прибавить сюда 4 на боковой грани, то это дает сумму, равную 5. Сумма оставшихся чисел на боковых гранях (5, 2 и 3) равна 10, что дает другому игроку преимущество в 5 очков.

В шестеричной системе число 109 778 запишется как 2 204 122. Цифра справа представляет единицы, следующая цифра дает число шестерок, третья справа цифра означает число «тридцатишестерок», четвертая цифра показывает число «порций» по 216 и т. д. Эта система основана на степенях 6 вместо степеней 10, как это имеет место в десятичной системе счисления.

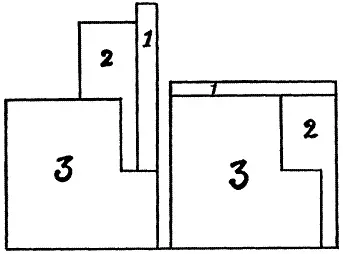
229. Задачу плотника можно решить, распилив доску на 3 части, как показано на рисунке.

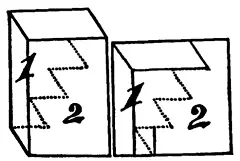
230. Дети купили 3 шоколадные конфеты, 15 шоколадных драже и 2 леденца.

231. С первого взгляда кажется, что общий улов может выражаться любым числом от 33 до 43, поскольку А может получить от 0 до 11 рыб, и доли других становятся очевидными. Однако, поскольку в итоге каждый мальчик получил одинаковое число рыб, ясно, что общая сумма должна равняться 35 или 40. Если мы возьмем последнее значение, то обнаружим, что выполнены все условия. А поймал 8 рыб, В – 6, С – 14, D – 4 и E -8 рыб. После того как В, С и D объединили свой улов и взяли по одной трети, у каждого из них оказалось по 8 рыб. Независимо от того, как мальчики объединяли и делили свою добычу, доля каждого останется равной 8 рыбам.

232. Ответ показан на рисунке.

233. Пирог тетушки Мэри можно разрезать на 22 части, как показано на рисунке.

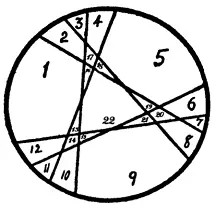
[Эта классическая задача представляет дополнительный интерес для тех, кого интересует формула, по которой можно вычислять максимальное число частей при заданном числе разрезов. – М. Г.]

234. Шелк продавался по цене 5 центов за моток, а шерсть – по 4 цента за моток.

235. В начале пути следы левой и правой ног Санта Клауса легко различимы. Проследив за их последовательностью, вы обнаружите, что след левой ноги Санта Клауса оказывается там, где должен быть след правой. Другими словами, Санта Клаус где-то сделал лишний шаг. Наиболее подходящее объяснение состоит в том, что он пробежал по первому маленькому кругу дважды, ступая точно в свой след.

236. Телль выбивает 100 очков, попав дважды в 11 и 6 раз в 13. Тень столбика от сетки у ноги Телля равна половине высоты столбика. Тень столба имеет в длину 35 ярдов, так что сам столб должен быть высотой в 70 ярдов, или 210 футов.

237. [У С. Лойда нет ответа на эту трудную задачу. Лучший способ поскорее закончить путешествие, согласующийся с подходом к аналогичным задачам Генри Э. Дьюдени, по-видимому, следующий.

Самый медленный пешеход С всю дорогу едет на тандеме. Вместе с А, самым быстрым пешеходом, он проезжает 31,04 мили, пока В идет пешком. Затем А слезает с велосипеда, а С возвращается, подбирает В в месте, расположенном в 5,63 мили от старта. Оставшуюся часть пути В и С проезжают на тандеме, прибывая в конечный пункт одновременно с А. Общее время путешествия составит чуть менее 2,3 часа.

Задачу можно решить алгебраическим путем, обозначив через х расстояние, пройденное 2? а через у расстояние, пройденное А. Приравнивая время, за которое В проходит х, ко времени, за которое велосипед доезжает до места высадки А и возвращается к В, мы получим одно уравнение, Второе уравнение удается получить, приравнивая время, за которое А проходит у, ко времени, за которое велосипед проделывает остальную часть путешествия. Мы решаем эти два уравнения, а остальное уже очевидно. – М. Г. ]