Сэм Лойд - Самые знаменитые головоломки мира

Теперь, обозначив через у расстояние от станции до Пайктауна, мы можем выписать два уравнения относительно х и у. В первом уравнении мы приравняем время, которое требуется человеку, чтобы пройти все расстояние минус 1 милю, ко времени, которое нужно дилижансу, чтобы проехать все расстояние плюс 30 мин. Во втором уравнении мы приравняем время перехода человека от станции до Пайктауна плюс 15 мин ко времени, за которое дилижанс преодолеет то же самое расстояние плюс 30 мин. Решая уравнения, мы получим для х значение, равное 6, а для у – равное 3, так что расстояние от гостиницы до Пайктауна составляет 9 миль. Дилижанс едет со скоростью 6 миль в час, а скорость человека равна 4 милям в час. – М. Г.]

180.Два кувшина уравновешиваются тремя блюдцами, так что вес одного блюдца равен 2/3 веса кувшина. Теперь добавим на каждую чашу весов второго рисунка по стакану; при этом в левой чаше окажутся те же предметы, что и в левой чаше первого рисунка. Это означает, что вес кувшина равен весу блюдца и двух стаканов, а поскольку вес блюдца равен 2/3 веса кувшина, то вес двух стаканов равен оставшейся 1/3 Следовательно, вес каждого стакана равен 1/6 веса кувшина.

На первом рисунке мы видим, что стакан (1/6 веса кувшина) и бутылка уравновешивают кувшин; отсюда мы находим, что вес бутылки составляет 5/6 веса кувшина. Таким образом, чтобы уравновесить бутылку на последнем рисунке, требуется 5 стаканов.

181. Дополнительное количество спиртного, купленное агентом, увеличило стоимость всего запаса до 343 долларов. К этой сумме он сделал надбавку в 10 %, что привело к общей продажной стоимости, равной 377,3 доллара. Агент продал спиртного на 285,8 доллара, а на руках у него осталось напитков на 91,5 доллара, как и показано на рисунке. Стоимость этого остатка без 10 %-й надбавки составляет 83,18 доллара. Вычитая ее из 343 долларов (общей стоимости спиртного), мы находим стоимость проданного спиртного – 259,82 доллара. Мы вычитаем это значение из общей продажной стоимости в 285,8 доллара и находим, что доход города на продаже спиртного составил 25,98 доллара.

Это можно проверить следующим образом. Доход в 25,98 доллара плюс аванс в 12 долларов и 59,5 доллара стоимости напитков дают в сумме 97,48 доллара. Отсюда мы вычитаем комиссионные агента, равные 14,29 доллара, что дает стоимость оставшегося спиртного в 83,19 доллара и показывает, что расчеты агента были правильными в пределах 2 центов.

182. У леди в начале прогулки было 42 цента.

183. Дети были настолько не в ладах с календарем, что отправились в школу воскресным утром!

184.[Пусть х означает общее число столбов, а у – число часов, за которое автомобиль проезжает 3 5/8 мили. Автомобиль минует х столбов за у часов, то есть х/у столбов в час, или х /60 у столбов в минуту. Поскольку нам известно, что число столбов, мимо которых автомобиль проезжает за минуту, умноженное на 3 5/8, равно его скорости, выраженной в милях в час, мы можем составить следующее уравнение: 3 5/ 8 х / 60у = 3 5/ 8 / у.

Произведя сокращение на общий множитель в левой и правой частях, мы находим, что х = 60.

Поскольку линия длиной в 3 5/8 мили, или в 19 140 футов, [35]содержит 60 столбов, то, разделив 19 140 на 60, мы находим, что расстояние между двумя соседними столбами составляет 319 футов. Скорость автомобиля, как и длина линии, оказывается не существенной. Однако решение задачи не единственно, если только мы не предположим, что счет столбов, проезжаемых за минуту, начинается и заканчивается в точке, расположенной в промежутке между столбами, и что аналогично определяется и длина телеграфной линии. – М. Г.]

185. Вот эти 5 нечетных «цифр», которые в сумме дают 14:

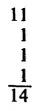
186. На рисунке показан ответ к этой удивительно трудной головоломке.

187. Шахматную доску можно разделить на 18 различных частей, как показано на рисунке.

[Существует много разных способов, какими можно разделить доску на 18 различных частей. В качестве интересного упражнения читатель может попытаться найти доказательство того, что 18 – действительно максимальное число. – М. Г.]

188. Котелок, подобно абажуру, имеет форму усеченного конуса, у которого верхушка отрезана плоскостью, параллельной основанию. Объем такой фигуры можно найти, вычитая из объема конуса объем отрезанной части, или проще по формуле:

πh/3(R 2+ r 2+ Rr).

В этой формуле h означает высоту усеченного конуса, а r и R – соответственно радиусы верхнего и нижнего оснований. В нашем случае высота котла равна 12 дюймам, и один из радиусов вдвое больше другого. Если мы через R обозначим радиус дна, то радиус крышки будет равен 2 R , а объем – 28π/R 2. Поскольку объем равен 25 галлонам, то есть 5775 кубическим дюймам, легко найти диаметр обода, а тем самым и крышки – он чуть превышает 32 дюйма.

189. Каждую неделю добрая леди тратила на благотворительные цели 120 долларов. Первоначально еженедельное «пособие» получали 20 человек.

190. Один из способов образовать нужные 8 дробей состоит в следующем (некоторые из чисел можно слегка изменять и все же получить те же самые дроби).

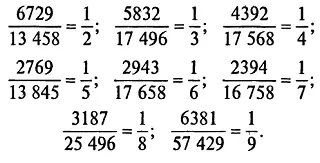
191. В цирке было 14 лошадей и 22 наездника. Таким образом, на долю зверинца приходится 56 ног и 20 голов. На рисунке можно насчитать 10 животных и 7 птиц, что дает 17 голов и 54 ноги. Значит, остаются неучтенными 3 головы и 2 ноги. Не требуется особенно живого воображения, чтобы понять: в клетке, привлекшей столько народу, должен находиться индийский заклинатель змей с двумя кобрами.

192.Фермер Джонс начал торговлю, имея 719 дынь. Из них 576 дынь он продал по 1 доллару за дюжину (48 долларов), а оставшиеся 143 – по одному доллару за 13 штук (11 долларов), что принесло ему доход в 59 долларов за все 719 дынь.

[Треугольную пирамиду из 120 дынь вместе с треугольной пирамидой из 560 дынь можно превратить в одну треугольную пирамиду, содержащую 680 дынь. Общая формула для этих тетраэдрических чисел имеет вид 1/6n(n + l)(n + 2). – M. Г.]

193. Каждый из молодых людей начал с 25 долларов. Джим поставил 15 долларов при общей ставке 15 против 1 и выиграл 225 долларов, так что его капитал вырос до 250 долларов. Джек поставил 10 долларов при общей ставке 10 против 1 и выиграл 100 долларов, что принесло ему капитал в 125 долларов, то есть ровно половину капитала Джима.