W Cat - Описание языка PascalABC.NET

Таким образом, решение задачи будет иметь следующий вид:

usesPT4;

functionNodeCount(P: PNode): integer;

begin

ifP = nil then

result := 0

else

result := 1 + NodeCount(P^.Left) + NodeCount(P^.Right);

end;

varP1: PNode;

begin

Task('Tree2');

read(P1);

write(NodeCount(P1));

end.

Цепочка рекурсивных вызовов функции NodeCount завершается при достижении терминальной вершины (листа), у которой поля Left и Right равны nil. Благодаря наличию функции NodeCount, раздел операторов программы является очень кратким: в нем считывается адрес P1 корня исходного дерева, после чего вызывается функция NodeCount(P1), возвращаемое значение которой сразу выводится процедурой write.

Запустив эту программу пять раз, мы получим сообщение Задание выполнено ! ".

Рассмотренная выше реализация бинарных деревьев позволяет легко переходить от родительских вершин к их дочерним вершинам, но не допускает обратного перехода. В то же время, для некоторых задач, связанных с обработкой деревьев, возможность обратного перехода от потомков к их предку позволяет получить более простое решение. Ясно, что для обеспечения возможности обратного перехода каждую вершину дерева надо снабдить еще одним полем связи, в котором должна храниться ссылка на ее родительскую вершину. Это поле связи естественно назвать Parent. Поскольку корень дерева предка не имеет, его поле Parent должно быть равно nil.

Деревья, вершины которых содержат информацию о своих родителях, будем называть деревьями с обратной связью . Особенности работы с подобными деревьями рассмотрим на примере задания Tree49.

Tree49°. Дан указатель P 1на корень дерева, вершинами которого являются записи типа TNode, связанные между собой с помощью полей Left и Right. Используя поле Parent записи TNode, преобразовать исходное дерево в дерево с обратной связью , в котором каждая вершина связана не только со своими дочерними вершинами (полями Left и Right), но и с родительской вершиной (полем Parent). Поле Parent корня дерева положить равным nil.

Запустив программу-заготовку, созданную для задания Tree49, мы увидим в области исходных данных изображение обычного" бинарного дерева, в то время как в области результатов будет изображено дерево с обратной связью, вершины которого связаны не одинарными, а двойными линиями.

Обратите также внимание на то, что в области результатов отсутствуют какие-либо данные, кроме измененного дерева. Это означает, что в программе, решающей задачу, не требуется использовать процедуры вывода; достаточно лишь преобразовать исходное дерево требуемым образом. Поскольку при таком преобразовании адрес корня дерева P 1не изменится, задачник сможеть получить доступ к этому дереву и проверить его правильность.

Для преобразования исходного дерева в дерево с обратной связью необходимо задать правильные значения для полей Parent всех вершин дерева, перебирая эти вершины с помощью подходящей рекурсивной процедуры. В эту процедуру удобно передавать в качестве параметров не только указатель P на текущую вершину, но и указатель Par на предка этой вершины:

usesPT4;

procedureSetParent(P, Par: PNode);

begin

ifP = nil then

exit;

P^.Parent := Par;

SetParent(P^.Left, P);

SetParent(P^.Right, P);

end;

varP1: PNode;

begin

Task('Tree49');

read(P1);

SetParent(P1, nil);

end.

При стартовом запуске рекурсивной процедуры SetParent в качестве второго параметра указывается nil.

Примечание.Обозначение для двойной связи может оказаться полезным при анализе ошибочного решения. Так, если в изображении дерева с обратной связью имеется вершина, соединенная со своей родительским вершиной не двойной, а одинарной линией, значит, у этой вершины поле Parent содержит ошибочное значение (например, равно nil).

С помощью связанных записей типа TNode можно моделировать не только бинарные деревья, но и произвольные упорядоченные деревья, вершины которых имеют любое число непосредственных потомков (будем называть такие деревья деревьями общего вида ; для них также используется название деревья с множественным ветвлением"). Рассмотрим задание Tree86 -- первое из заданий, связанных с деревьями общего вида, в котором описываются особенности подобных деревьев.

Tree86°. Дерево общего вида (каждая вершина которого может иметь произвольное число дочерних вершин, расположенных в фиксированном порядке в направлении слева направо) реализуется с помощью набора связанных записей типа TNode следующим образом: для каждой внутренней вершины ее поле Left содержит указатель на ее первую (т. е. левую) дочернюю вершину, а поле Right -- указатель на ее правую сестру , т. е. вершину, имеющую в дереве общего вида того же родителя. Поле Right корня дерева общего вида всегда равно nil, так как корень сестер не имеет. Дан указатель P 1на корень непустого бинарного дерева. Создать дерево общего вида, соответствующее исходному бинарному дереву, и вывести указатель P 2на его корень.

Приведем пример дерева общего вида, которое реализовано с помощью связанных записей типа TNode (аналогичным образом деревья общего вида изображаются в окне задачника):

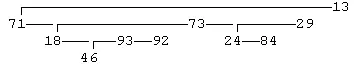
Корень этого дерева (со значением 13) имеет три дочерние вершины (71, 73 и 29), причем вершина 71 не имеет потомков, вершина 73 имеет три непосредственных потомка (18, 93 и 92), а вершина 29 -- два (24 и 84). На последнем уровне располагается вершина 46, являющаяся единственной дочерней вершиной вершины 93.

При ознакомительном запуске задания Tree86 на экране появится окно, подобное следующему.

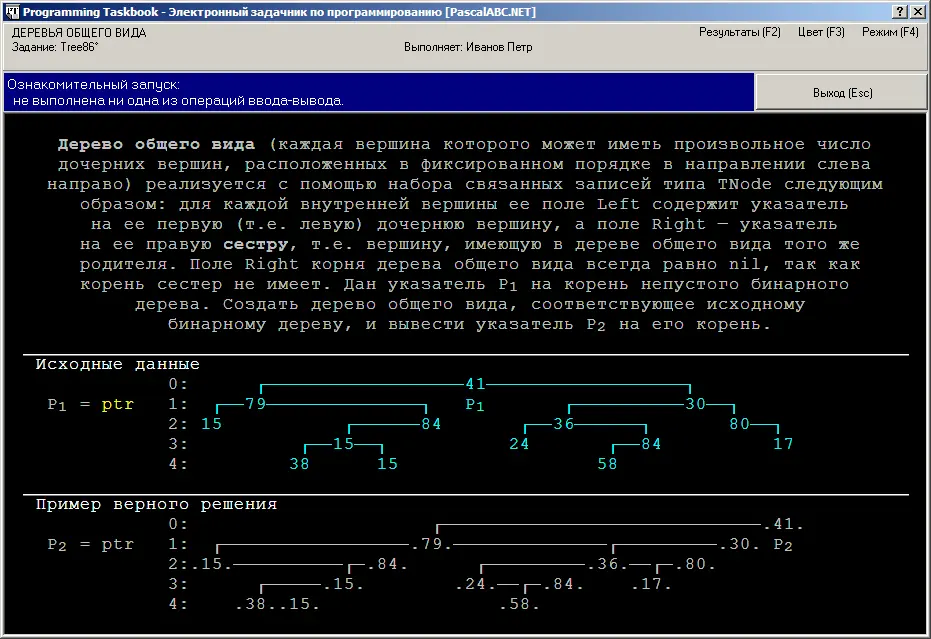
Обратите внимание на то, как выглядит одно и то же дерево в двух различных представлениях: вариант, соответствующий обычному бинарному дереву, приводится в разделе исходных данных, а вариант, соответствующий дереву общего вида, -- в разделе результатов. При переходе от бинарного дерева к дереву общего вида часть информации о структуре бинарного дерева теряется, поскольку в случае, если некоторая вершина дерева общего вида имеет только одного непосредственного потомка, нельзя определить, каким был этот потомок в исходном бинарном дереве -- левым или правым.