Инесса Раскина - Логика для всех. От пиратов до мудрецов

(2) Клад находится от пальмы не в 30 футах к востоку или не в 120 футах к северу.

Все просто: каждое простое высказывание заменено противоположным, а связка «и» заменена на «или».

Вообще, отрицанием к высказыванию «А и Б» служит высказывание «не А или не Б».

Отрицанием к высказыванию «А или Б» служит высказывание «не А и не Б».

Последние два предложения называются законами де Моргана. Но названы они так вовсе не в честь самого знаменитого пирата Карибского моря Генри Моргана, а в честь жившего на два века позже шотландского математика Огастеса де Моргана.

Задача 4.5.Постройте отрицания к высказываниям Бена, Вилли и Глена. Какие из этих отрицаний истинны?

Решение.Сразу можно сказать, что отрицания к ложным высказываниям Бена и Вилли сами будут истинными высказываниями, а отрицание к истинному высказыванию Глена будет ложным. Вот эти отрицания:

Бен: Клад находится от пальмы не в 100 футах к востоку или не в 120 футах к северу.

Вилли: Клад находится от пальмы не в 30 футах к востоку или не в 100 футах к северу.

Глен: Клад находится от пальмы не в 100 футах к востоку или не в 100 футах к северу.

Задача4.6. Замените высказывания на противоположные:

1) Но с ветром худо и в трюме течи.

2) Ни Бог, ни дьявол не помогут ему спасти свои суда.

3) Случился штиль иль просто ветер встречный.

4) Вода и ветер сегодня злы, и зол, как черт, капитан.

Ответ.1) С ветром все в порядке или трюм не течет.

2) Бог или дьявол помогут ему спасти его суда.

3) Не случилось ни штиля, ни встречного ветра.

4) Хотя бы один из трех: вода, ветер, капитан – сегодня добр.

Вот, пожалуй, и все, чему стоило поучиться у пиратов. Больше возвращаться на остров незачем: Глен вот-вот найдет клад, а на то, что произойдет после этого, детям до 18 лет смотреть не стоит. Как, впрочем, и взрослым. Вместо клада нас ждут…

Задачи для самостоятельного решения

Задача4.7. В ансамбль приглашают всех, кто хорошо поет или танцует. Наташа хорошо и поет, и танцует. Пригласят ли ее в ансамбль?

Задача 4.8.Каждый из четырех гномов: Беня, Сеня, Веня и Женя – либо всегда говорит правду, либо всегда врет. Мы услышали такой разговор:

Беня – Вене: «Ты врун».

Женя – Бене: «Сам ты врун!»

Сеня – Жене: «Да оба они вруны!» Подумав, он добавил: «Впрочем, ты тоже».

Кто из гномов говорит правду?

Задача4.9. Математик с тремя детьми пришел в пиццерию.

– Хочу, чтобы в пицце были помидоры или грибы, – потребовала Аня.

– Пиццу с помидорами и грибами я есть не буду, – заявил Боря.

– Если будут помидоры, а грибов не будет, то я не буду есть, – добавил Ваня.

– Отлично! – воскликнул математик. – Сделайте нам, пожалуйста, пиццу с…

Так какую же пиццу заказал математик, чтобы все дети ее ели?

Задача 4.10.Андрей является участником шоу-викторины. Главный приз спрятан в одном из ящиков. Андрей получает 4 подсказки:

1. Приз находится в синем или зеленом ящике.

2. Приз находится в красном или желтом ящике.

3. Приз находится в зеленом ящике.

4. В желтом ящике приза нет.

Три подсказки ошибочны и только одна правильная. Андрей поразмыслил и открыл правильный ящик. Ящик какого цвета он выбрал?

Задача 4.11.В доме 300квартир. В квартиры, номера которых кратны 4 или 6, Дед Мороз принес шоколадку. А в квартиры, номера которых кратны 4 и 6, – айфон. Чего Дед Мороз принес в дом больше – айфонов или шоколадок? Во сколько раз?

Задача 4.12.Зайчишка-хвастунишка залез на пенек и громко закричал: «Во всем лесу нет никого меня смелее, нет никого меня умнее!». Он, конечно же, соврал. Какой из пяти выводов можно сделать?

(A) Все в лесу умнее и смелее его.

(Б) В лесу есть кто-то и умнее его, и смелее.

(B) В лесу есть кто-то его умнее.

(Г) В лесу есть кто-то его смелее.

(Д) В лесу есть кто-то умнее или смелее его.

Задача 4.13.Король подвел узника к двум дверям, ведущим в две комнаты. В каждой из них может находиться принцесса или тигр. При этом не исключено, что в обеих комнатах находятся принцессы или в обеих – тигры. Узник должен войти в одну из комнат. Если там окажется принцесса, то узник женится на ней. Если тигр – то он растерзает узника. На дверях висят таблички с надписями:

Король любезно сообщил, что на одной из табличек написана правда, а на другой – нет. Какую комнату вы посоветуете выбрать?

Задача 4.14.Другого узника ожидало похожее испытание. Но на этот раз король сказал, что утверждения на обеих табличках одновременно либо истинны, либо ложны. А написано было вот что:

В какую дверь следует идти узнику?

Задача 4.15.Для третьего узника король повесил на обе двери одинаковые таблички:

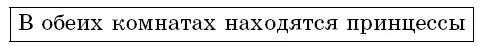
А сказал так: «Если в левой комнате находится принцесса, то утверждение на табличке истинно, если же тигр, то ложно. В правой же комнате все наоборот: утверждение ложно, если там находится принцесса и истинно, если тигр». Куда лучше идти узнику?

Задача 4.16.Один из пяти братьев испек маме пирог.

Никита сказал: «Это Глеб или Игорь».

Глеб сказал: «Это сделал не я и не Дима».

Игорь сказал: «Вы оба шутите».

Антон сказал: «Нет, один из них сказал правду, а другой обманул».

Дима сказал: «Нет, Антон, ты не прав».

Мама знает, что трое из ее сыновей всегда говорят правду. Кто испек пирог?

Задача 4.17.Четверо детей сказали друг о друге так:

Маша: «Саша, Наташа и Гриша умеют сидеть на стуле».

Саша: «Маша, Наташа и Гриша не умеют сидеть на стуле».

Наташа: «Маша и Саша солгали».

Гриша: «Маша, Саша и Наташа сказали правду».

Сколько детей на самом деле сказали правду?

Задача 4.18.«Хоп!» – это игра на внимательность. Игроки по очереди называют натуральные числа в порядке возрастания. Если число кратно 3 или содержит в записи цифру 3, то вместо него надо сказать «Хоп!». Если не ошибаться, получится ряд: 1, 2, хоп, 4, 5, хоп, 7, 8, хоп, 11, хоп, хоп, 14 и т. д. Кто по ошибке назовет запрещенное число, выходит из круга. Побеждает последний оставшийся игрок.

Пять ребят играли в «Хоп!». Известно, что числа 1 и 23 назвал Петя, 2 и 20 – Вася, а 5 и 15 – Таня. Сколько раз победитель сказал «Хоп!»?