Николай Горькавый - Колумбы Вселенной (сборник)

– Я не знаю, что такое тангенс! – насупилась Галатея.

– Тангенс – это очень простая штука, я сейчас объясню, – сказал Майкл. – Вот смотри, предположим, что длина нашей тени равна длине зонтика. Чему равен верхний угол в таком треугольнике?

– Это я знаю, – облегченно сказала Галатея. – Такой треугольник стал половиной квадрата, значит, верхний угол стал равен половине прямого угла, или 45 градусам.

– Верно! – просиял Майкл и быстро написал на листке бумаги слева 45 градусов, а справа единицу – результат деления тени на зонтик. – А если длина тени стремится к нулю, то и угол равен нулю! – И Майкл добавил два нуля в таблицу – только в самый низ страницы. – Теперь будем задаваться другими значениями отношения длины тени и зонтика – от единицы до нуля, а потом станем измерять получившиеся углы. Так мы заполним все строчки в таблице. Например, для длины тени вползонтика мы можем измерить верхний угол – и он окажется равным 26,6 градуса. Можешь ли ты, Галатея, заполнить такую таблицу сама, если я дам тебе линейку для черчения треугольников и угломер для измерения углов?

– Конечно, могу, – заявила Галатея. – Это и кошка смогла бы сделать.

– Прекрасно! – улыбнулся Майкл. – Теперь представь, что какой-то древний математик сделал это впервые, посмотрел на получившуюся таблицу и сказал: «Отношение горизонтальной и вертикальной сторон в таком прямоугольном треугольнике является функцией верхнего угла. Отныне пусть эта функция называется тангенсом !»

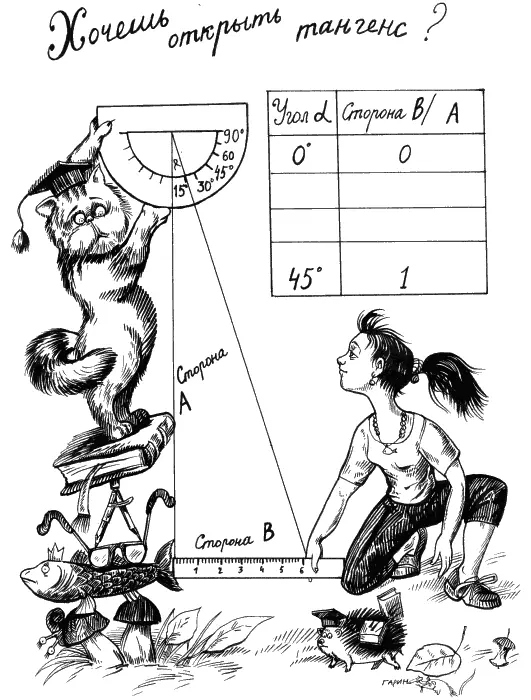
– Вот так просто? – не поверила ушам Галатея. – Взять составить таблицу примитивных измерений и объявить это тангенсом?

– Да, только надо сделать это первым. А потом надо ввести эту таблицу во все калькуляторы. И теперь, когда я сообщаю калькулятору, что верхний угол в моём треугольнике равен 29 с половиной градусов, то он сразу сверяется с таблицей тангенсов и отвечает, что длина тени составляет… э-э-э… примерно 56,5 процента от длины зонтика.

– Если я возьму и составлю таблицу верхнего угла и отношений горизонтальной тени не к длине зонтика, а к длине наклонной линии в этом треугольнике, это ведь будет другая функция? – спросила недоумевающая Галатея.

– Конечно! – воскликнул Майкл. – Это будет функция, которая называется синусом ! Ты самостоятельно переоткрыла новую тригонометрическую функцию!

Галатея польщенно хмыкнула и напряженно впилась взглядом в таблицу.

– Неужели до сих пор не понятно? – поддел её Андрей. – Кошка бы уже поняла!

Потом он повернулся к Майклу и спросил:

– Значит, арктангенс – это наша таблица, только читаемая в другую сторону?

Майкл согласился:

– Да, я могу сначала посмотреть на отношение длины зонтика и тени, а потом найти по таблице величину верхнего угла. Эта процедура будет называться вычислением арктангенса .

– Постойте-постойте! – воскликнула Галатея. – Объясните мне вот что…

Дети спорили про синусы и тангенсы до тех пор, пока не принесли вкуснейшие пирожные и душистый чёрный чай с мятой. А Дзинтара наклонилась к Майклу и тихо сказала:

– Спасибо за то, что открыл для детей тангенс!

Пока то да сё – время пролетело, и позвонил Роберт.

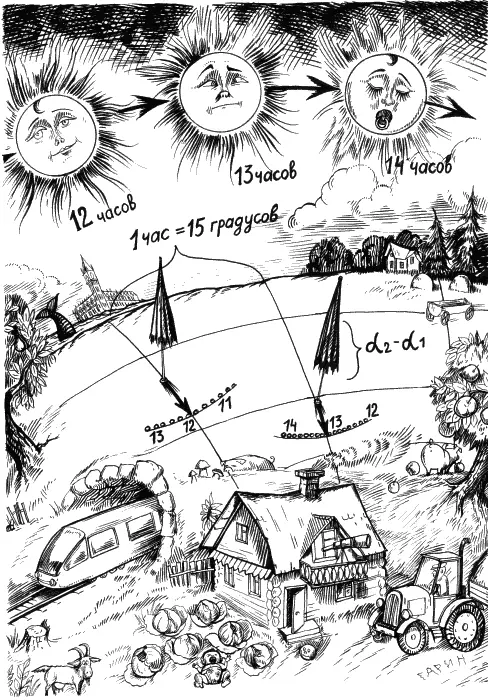
– У нас Солнце достигло максимальной высоты в 1 час и 4 минуты!

Майкл уточнил:

– По гринвичскому времени, которое отстаёт от нашего на целый час, так как располагается в другом часовом поясе?

– Да.

– Итак, гринвичский полдень настал позже нашего на 1 час и 4 минуты. Земля делает оборот в 360 градусов за 24 часа. Следовательно, запаздывание максимального подъёма Солнца на один час соответствует смещению по долготе на 15 градусов, а запаздывание на 4 минуты – на один градус. Значит, между нами и Гринвичским меридианом расположено примерно 16 градусов. А так как долгота Гринвичского меридиана, по взаимному соглашению, – ноль, то это означает, что наша долгота – 16 градусов восточной долготы. Роберт, а какой угол отбрасывала ваша тень в этот момент?

– 41,5 градуса отклонения от вертикали.

– А у нас 29,5. Значит, разница в широтах между нами и Гринвичем – 12 градусов. Каждый моряк знает, что широта Гринвича – 51,5 градуса, и легко найдёт нашу широту – 39,5 градуса северной широты. Если бы у меня были таблицы, в которых было бы указано время достижения максимальной высоты Солнца в Гринвиче каждый день, то я бы смог определить свои координаты без звонка Роберту. Такими таблицами, предсказывающими положение Солнца на год вперёд, и пользовались моряки прошлых веков, замеряя по своим часам время максимальной высоты Солнца в неведомых краях, куда их заносила судьба моряка.

– Здорово! – восхищённо сказал Андрей.

А Галатея недоверчиво покачала головой, попросила принести карту Европы и поползла – или поплыла? – по ней, пыхтя, как древний паровой буксир. Потом спросила:

– Предположим, что мы перелетели из Бельведере-Мариттимо в Валенсию, которая расположена на нашей широте, но возле нулевой долготы. Солнце в Лондоне и в Валенсии достигнет максимальной высоты одновременно?

– Да, между этими городами существует лишь разница в широте. Кстати, ты можешь определить по карте расстояние между Валенсией и Лондоном?

Галатея с помощью линейки и Андрея измерила расстояние между английским Лондоном и испанской Валенсией:

– 1335 километров!

– Отлично! – обрадовался Майкл. – А вот теперь догадайтесь, как можно определить длину окружности Земли, зная, что между широтами Лондона и Валенсии разница в 12 градусов, а расстояние между этими городами составляет 1335 километров? Такую задачку в своё время решил Эратосфен – для двух египетских городов, расположенных примерно на одной долготе.

Дети задумались. Первым сообразил Андрей:

– 12 градусов – это одна тридцатая окружности в 360 градусов! Значит, длина земной окружности в 30 раз больше, чем расстояние между Лондоном и Валенсией. Это будет… 1335 умножить на 30… это будет 40 тысяч километров и ещё… ещё 50 километров!

Майкл восхитился:

– Прекрасный, очень точный результат!

Галатея немедленно надулась на Андрея. А тот сказал:

– Оказывается столько интересного можно узнать, всего лишь измеряя длину тени!

Майкл, кивнув, сказал:

– Астрономическая обсерватория необязательно должна оснащаться телескопом. Даже с помощью простейших приборов можно сделать ценные астрономические измерения. Если определять длину тени на земле в течение года, как это делали древние, то можно вычислить важнейшие астрономические параметры Земли – например, узнать наклон её оси вращения.