Дж. Кеоун - OrCAD PSpice. Анализ электрических цепей

Итак, мы рассмотрели зависимые источники четырех типов E (VCVS или ИНУН — источник напряжения, управляемый напряжением), F (CCCS или ИТУТ — источник тока, управляемый током), G (VCCS или ИТУН — источник тока, управляемый напряжением) и H (CCVS или ИНУТ — источник напряжения, управляемый током). Зависимые источники играют важную роль при анализе большинства схем с активными приборами, такими как транзисторы. Они дают возможность достаточно просто рассчитывать такие схемы, открывая путь к пониманию работы сложных устройств. При этом основные идеи лучше всего можно понять при исследовании цепей постоянного тока, которое проводится в данной главе.

Материал этой главы обычно не включается в общие программы обучения. Если полиномиальные источники не интересуют вас в настоящий момент, вы можете пропустить этот раздел, перейдя сразу к разделу, посвященному методу контурных токов.

Возможности применения для анализа нелинейных зависимых источников лучше всего рассмотреть на конкретном примере, приведенном на рис. 1.29. На нем показан источник напряжения V , питающий два последовательно включенных резистора R 1= R 2=1 кОм. Источник ИНУН обозначен как Е , но в нашем случае напряжение Е связано с управляющим напряжением не просто постоянным коэффициентом k. Предполагается, что Е связано с напряжением V 20нелинейной зависимостью, задаваемой полиномом

Рассмотрим теперь, как вводятся в командной строке, использующей зависимые источники (POLY), управляемые более чем одним напряжением. В примере, представленном на рис. 1.29, сделаем Е функцией сразу двух напряжений v 1и v 2. Для этого в командной строке следует записать POLY(2) 2,0 4,0. Запятые приведены для ясности и могут быть опущены. В оставшейся части строки должны быть приведены коэффициенты. При двух управляющих напряжениях необходимо ввести шесть коэффициентов: k 0, k 1 v 1 , k 2 v 2, k 3 v 1² , k 4 v 1 v 2и k 5 v 2² . Эта последовательность более сложна и требует некоторого изучения. Коэффициенты k представляют собой множители для каждого возможного напряжения и для их комбинаций. Напряжения перечисляются в порядке возрастания степени, начиная с первого напряжения, обозначенного как v 1. В нашем примере v 1является напряжением V 20, a v 2представляет собой V 40.

Приведем теперь командную строку, вводящую источник, управляемый двумя напряжениями:

Е 3 0 POLY(2) 2,0 4,0 0 2 3

Последние три значения (0 2 3) представляют собой значения коэффициентов k 0, k 1и k 2. Они устанавливают полином (0+2 v 1+3 v 2). Таким образом, напряжение зависимого источника Е представляет собой сумму удвоенного падения напряжения на R 2и утроенного падения напряжения на R 4. Отметим снова, что запятые внесены для ясности и их можно опустить. Входной файл имеет вид:

Polynomial Form for Two Inputs

V 1 0 1V

E 3 0 POLY(2) 2,0 4,0 0 2 3

R1 1 2 1k

R2 2 0 1k

R3 3 4 2k

R4 4 0 2k

.DC V -4 4 1

.PRINT DC V(2) V(3) V(4)

.END

Запустим моделирование и убедимся, что Е задается выражением (2 V 20+3 V 40). Вы можете использовать такой зависимый источник в схемах, в которых появляются суммы, разности или произведения различных токов и напряжений. Использование зависимых источников типа Е, F, G и Н с обозначением POLY позволяет моделировать источники, получая выходные файлы, подобные приведенному на рис. 1.31.

**** 07/27/05 10:54:26 ******** Evaluation PSpice (Nov 1999) **********

Polynomial Form for Two Inputs

**** CIRCUIT DESCRIPTION

V 1 0 1V

E 3 0 POLY(2) 2,0 4,0 0 2 3

R1 1 2 1k

R2 2 0 1k

R3 3 4 2k

R4 4 0 2k

.DC V -4 4 1

.PRINT DC V(2) V(3) V(4)

.END

**** 07/27/05 10:54:26 ******* Evaluation PSpice (Nov 1999) ***********

Polynomial Form for Two Inputs

**** DC TRANSFER CURVES TEMPERATURE = 27.000 DEG С

V V(2) V(3) V(4)

-4.000E+00 -2.000E+00 8.000E+00 4.000E+00

-3.000E+00 -1.500E+00 6.000E+00 3.000E+00

-2.000E+00 -1.000E+00 4.000E+00 2.000E+00

-1.000E+00 -5.000E-01 2.000E+00 1.000E+00

0.000E+00 0.000E+00 0.000E+00 0.000E+00

1.000E+00 5.000E-01 -2.000E+00 -1.000E+00

2.000E+00 1.000E+00 -4.000E+00 -2.000E+00

3.000E+00 1.500E+00 -6.000E+00 -3.000E+00

4.000E+00 2.000E+00 -8.000E+00 -4.000E+00

Рис. 1.31. Вид выходного файла при анализе схемы на рис. 1.29 с двумя управляющими напряжениями

Традиционные курсы электротехники обычно излагают метод контурных токов, использующий контуры и контурные токи для вычисления токов в ветвях схемы.

Стандартная форма уравнений для трех контурных токов имеет вид:

R 11 I 1+ R 12 I 2+ R 13 I 3= V 1;

R 21 I 1+ R 22 I 2+ R 21 I 3= V 2;

R 31 I 1+ R 32 I 2+ R 31 I 3= V 3.

где R 11— собственное сопротивление контура 1; R 12— взаимное сопротивление контуров 1 и 2 ; R 13 — взаимное сопротивление контуров 1 и 3, а V 1— контурная ЭДС контура 1 ; алгебраическая сумма всех ЭДС, действующих в контуре 1 (положительными считаются ЭДС, направление которых совпадает с направлением обхода контура). Аналогично составлены уравнения и для контуров 2 и 3 . Ручной расчет системы трех уравнений с тремя неизвестными утомителен и часто приводит к ошибкам в вычислениях. Если же число уравнений больше трех, то вычислительная работа становится очень тяжелой. Для выполнения такой работы применяются многочисленные версии компьютерных программ.

А можно ли решить такую систему уравнений с помощью SPICE? Если рассматривать общий случай, то ответ будет отрицательным. Однако можно использовать некоторые приемы, чтобы выполнить такое моделирование, как в следующем примере (рис. 1.32). Здесь имеется три контура. Вы можете составить систему из трех уравнений в стандартном формате и вычислить затем I 1, I 2и I 3.

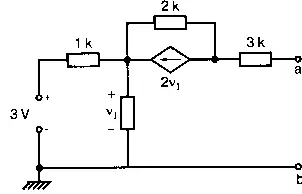
Рис. 1.32. Анализ методом контурных токов на PSpice

Вы можете сделать это и в качестве упражнения перед просмотром следующего входного файла:

Mesh Analysis with PSpice

V1 1 0 50V

V2 4 0 30V

R1 1 2 100

R2 2 0 200

R3 2 3 400

R4 3 0 200

R5 3 4 100

.OP

.OPT nopage

.DC V1 50 50 10

.PRINT DC I(R1) I(R2) I(R3)

.END

Во входной файл включены две интересные команды. Первая из них — это команда .DC. Это команда вариации по напряжению V 1, которая была введена при исследовании примера, касающегося теоремы Нортона. Она позволяет изменять напряжение V 1. Следующие два значения (50 и 50) задают начальное и конечное значение при вариациях. Поскольку они одинаковы, это практически означает отказ от вариации. Если же вы действительно хотите изменять напряжение с шагом от 10 до 50 В, то команду необходимо заменить следующей: