Дж. Кеоун - OrCAD PSpice. Анализ электрических цепей

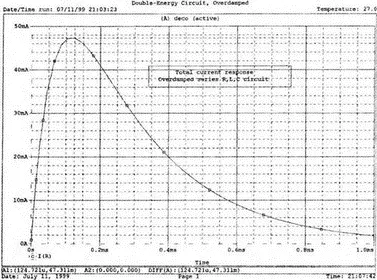
Рис. 6.11. Временные диаграммы напряжений на элементах схемы на рис. 6.9

Обратимся снова к схеме на рис. 6.9. Анализ показывает, что при критическом затухании

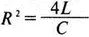
Если оставить значения L и С прежними, то условие критического режима соблюдается при R =160 Ом. Чтобы увидеть результаты, просто измените значение R во входном файле и выполните анализ снова.

Убедитесь, что ток достигает максимального значения i =55,36 мА при i =125 мкс. Удалите график тока и получите графики различных напряжений, как в предыдущем анализе. Эти кривые будут иметь тот же вид, что и при апериодическом процессе (рис. 6.12).

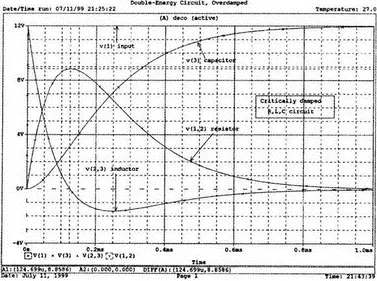
Рис. 6.12. Графики напряжений в схеме (рис. 6.9) при критическом затухании

Чтобы исследовать процесс при слабом затухании, уменьшим сопротивление до значения меньшего, чем критическое (160 Ом). Проведем анализ при R= 60 Ом. Изменим значение R во входном файле и рассмотрим график тока I(R). Убедитесь, что ток достигает максимума i =92,7 мА при t =111 мкс и становится сначала отрицательным, а затем снова положительным. Такой колебательный характер процесса типичен для случая слабого затухания. На рис. 6.13 показан график тока при колебательном процессе. Вы можете попробовать проанализировать процесс при меньших значениях сопротивления и выяснить влияние сопротивления на переходной процесс. Вы установите, что при меньших значениях R период колебаний увеличивается.

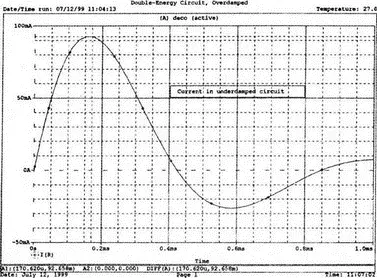
Рис. 6.13. График тока в схеме (рис. 6.9) при малом затухании

Удалите теперь график тока и получите графики напряжений V(1), V(3), V(2,3) и V(1,2). Эти графики показаны на рис. 6.14. Интересно отметить, что максимум напряжения на конденсаторе выше приложенного напряжения 12 В и достигается в момент минимума напряжения на катушке индуктивности. Наблюдая процесс при других значениях R, можно увидеть различные варианты взаимодействия составляющих напряжения, при этом, конечно, всегда соблюдается второй закон Кирхгофа.

Рис. 6.14. Графики напряжений для режима с малым затуханием

Определим, насколько похожа форма выходного напряжения на форму входного при подаче ступеньки напряжения на усилитель. Будем рассматривать усилитель как низкочастотный фильтр, схема которого показана на рис. 6.15.

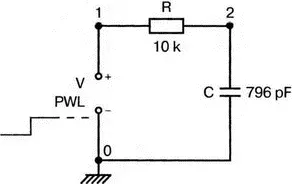
Рис. 6.15. Подача ступеньки входного напряжения на низкочастотный фильтр

Выходное напряжение изменяется по экспоненте на фронте и срезе импульса. На фронте выходное напряжение изменяется по формуле

v о= V (1 – e –t/RC ).

Время нарастания t r показывает, как быстро выходное напряжение может достичь максимума в ответ на ступеньку входного напряжения. Поскольку

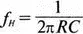
время нарастания

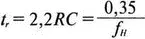
Чтобы избежать излишних искажений, мы предлагаем выбирать f H =1/ t p , где t p — ширина импульса. Это означает, что t r= 0,35 t p .

Чтобы показать эти свойства при f H =20 кГц, выберем следующие параметры модели низкочастотного фильтра: R =10 кОм, С =796 пФ. Из уравнений найдем t p =50 мкс и t r =17,5 мкс. Выясните, насколько близки эти значения к полученным при анализе на PSpice. Входной файл:

Pulse Response When fH=1/tp

V 1 0 PWL(0,0 0.5us, 1V 50us, 1V 50.5us,0)

R 1 2 10k

N 2 0 7 9 6pF

.TRAN 0.5us 100us

.PROBE

.END

Выполните анализ и получите в Probe графики входного v(1) и выходного v(2) напряжений. Проверьте по графику выходного напряжения, что t 0,1=1,1 мкс и t 0,9=18,6 мкс. Они представляют собой моменты времени, когда выходное напряжение составляет 0,1 и 0,9 от максимального значения. Разность между ними представляет собой время нарастания, равное tr =17,5 мкс, что соответствует результатам наших предварительных вычислений. Этот график приведен на рис. 6.16.

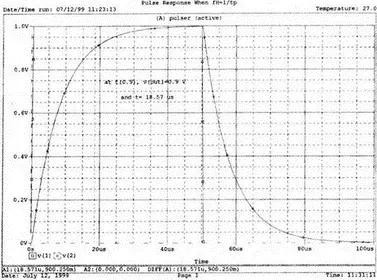
Рис. 6.16. Входное и выходное напряжения для схемы на рис. 6.15

Что будет, если мы вдвое увеличим емкость по сравнению с рекомендуемым максимальным значением? Выполните анализ с новым значением С =1,592 нФ. Убедитесь, что выходное напряжение не достигает значения 1 В и к тому же более искажено.

Сигнал передается гораздо лучше, когда емкость меньше рекомендуемого значения. Выполните анализ при С =398 пФ. Вы увидите, что в этом случае выходное напряжение намного правильнее воспроизводит прямоугольное входное напряжение.

При низкой частоте и, соответственно, большой длительности входных импульсов усилитель замещается высокочастотным фильтром (рис. 6.17), чтобы моделировать низкочастотный отклик усилителя. Уравнение для выходного напряжения:

v o = Ve -t|RC .

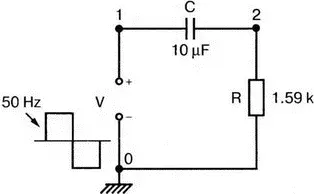
Рис. 6.17. Схема для исследования низкочастотного отклика

Когда постоянная времени τ= RC слишком мала, выходное напряжение имеет нежелательный спад. Поскольку значение R определяется входным сопротивлением усилительного каскада и не может изменяться, значение С должно быть выбрано достаточно большим, чтобы избежать чрезмерного наклона. Выберем, например, R= 1,59 Ом и С =10 мкФ и используем в качестве входного прямоугольное напряжение с частотой в 50 Гц. Входной файл для такого анализа:

Tilt of Square Wave for Low-Frequency Response

V 1 0 PWL(0,0 1us, 1V 10ms, 1V 10.001ms,-12V 20ms,-1V

+20.001ms,1V 30ms,1V)

N 1 2 10uF

R 2 0 1.59k

.TRAN 0,15ms 30ms

.PROBE

.END

Выполните анализ, затем получите графики v(1) и v(2). Найдите наклон выходного напряжения, сравнивая значения на фронте и на срезе импульса. Проверьте, что эти значения соответственно равны 1 и 0,533 В, создавая спад в 46,7%. Зачастую желательно, чтобы спад не превышал 10%. Очевидно, для этого необходимо увеличить значение емкости. Установите значение С =50 мкФ и выполните анализ снова. Проверьте, что спад не меньше чем 12%. Этот график показан на рис. 6.18.