Дж. Кеоун - OrCAD PSpice. Анализ электрических цепей

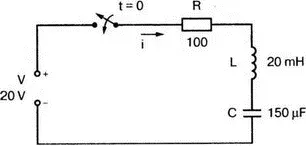
Рис. 6.37

6.4. а) Увеличьте значение R в задаче 6.3, чтобы создать критическое затухание, и получите графики токов и составляющих напряжений. Найдите максимальные положительные и отрицательные значения токов.

б) Задав значение R= 250 Ом, повторите предыдущее задание а). Найдите максимальные положительные и отрицательные значения всех составляющих напряжений.

6.5. На высоких частотах необходимо учитывать емкость на выходе усилителя напряжения. На рис. 6.38 выходная емкость составляет С =1 нФ и R= 10 кОм. При амплитуде приложенного напряжения в 1 В и t p= 100 мкс выходное напряжение должно быть достаточно близкой копией входного импульса.

а) Используйте метод, описанный в разделе «Отклик на единичное воздействие в усилителях», чтобы определить характер выходного напряжения. Используйте Probe, чтобы выяснить, является ли выходной импульс напряжения на конденсаторе С достаточно близкой копией входного импульса.

б) Если вы хотите получить более точную копию входного напряжения, попробуйте изменить значение t p и выполнить анализ снова. Каковы значения t H для пунктов а) и б) задания?

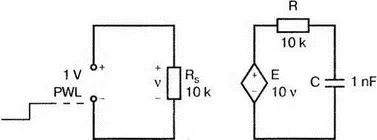
Рис. 6.38

6.6. При обсуждении низкочастотной реакции усилителя в этой главе мы установили, что обычно желательно, чтобы спад напряжения в конце импульса не превышал 10%. Приближенная формула для определения спада:

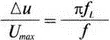
где t L =1/(2π RC ), а f — частота прямоугольного напряжения. Используйте методику, описанную в тексте, чтобы при воздействии прямоугольного напряжения с частотой 60 Гц найти следующее:

а) относительный спад выходного напряжения при R= 1,59 Ом и С =10 мкФ;

б) значение С , которое требуется, чтобы создать относительный спад приблизительно в 10%?

Проверьте ваши ответы с помощью графика, полученного в Probe.

Одна из сильных сторон PSpice заключается в способности анализировать системы с нелинейными характеристиками, например, исследовать усилитель мощности при подаче на его вход сигнала с высокой амплитудой. При этом усилитель начинает работать на нелинейной части характеристики, что приводит к искажениям в выходном напряжении. В этой главе мы выясним, насколько велики искажения, проанализировав гармонический состав выходного напряжения усилителя.

Начнем с простой схемы, позволяющей рассмотреть основные концепции, которые мы используем в дальнейшем для более сложных схем. На рис. 7.1 показано входное напряжение V BX.p= 1 В, это синусоидальная волна с частотой f =1 кГц и максимальным значением 1 В (действующим значением V вх =√2). Чтобы обеспечить выходное напряжение, которое является нелинейной функцией входного, в качестве усилителя используется источник напряжения Е, управляемый напряжением (ИНУН). В этом примере зависимость выходного напряжения от входного отображается функцией

f ( x ) = 1 + х + х ².

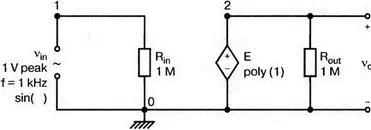
Рис. 7.1. Схема с нелинейной связью входного и выходного напряжений

Эта функциональная связь отображается в команде Е c помощью полиномиальных коэффициентов. Общий вид полинома:

f ( х ) = k 0+ k 1 х + k 2 х ².

Чтобы перейти к зависимости нашего примера, используем три последних числа команды ввода Е. Мы хотим провести гармонический анализ, чтобы увидеть, какие из гармоник присутствуют в выходном напряжении, но сначала попробуем определить, чего же мы должны ожидать.

Прежде чем перейти к разложению временных зависимостей в ряд Фурье, необходимо выполнить анализ для переходных процессов (программу transient analysis в PSpice).

Поэтому необходимо использовать обе команды .TRAN и .FOUR. Обычно выполняется анализ переходных процессов для полного периода основной частоты. В этом примере f =1 кГц; следовательно, Т =1/ f =1 мс. Гармонический анализ отражает частотные компоненты вплоть до девятой гармоники. Для большинства целей этого должно быть более чем достаточно. Если показывать более высокие гармоники, они не будут иметь большого значения из-за накопления ошибки округления в результатах.

Чтобы дать более подробное описание входного напряжения V BX , используем форму sin для описания источника. Параметры sin( а , b , с ,…) означают: а — постоянная составляющая, b — максимальное значение, с — частота, d — задержка, е — коэффициент затухания и f — фаза.

При включении во входной файл команды .FOUR производится гармонический анализ, дающий разложение в ряд Фурье для результатов анализа переходного процесса. Параметры для этой команды включают частоту основной гармоники и переменные, для которых будет получено разложение. В этом примере такими переменными будут периодические функции входного V(1) и выходного V(2) напряжений. Входной файл:

Fourier Analysis; Decomposition of Polynomial

Vin 1 0 sin(0 1 1000); аргументы для смещения, максимума и частоты

Rin 1 0 1MEG

Е 2 0 poly(1) 1,0 1 1 1; последние 3 значения для k0, k1, k2

Rout 2 0 1MEG

.TRAN 1us 1ms

.FOUR 1000 V(1) V(2)

.PROBE

.END

Проведите анализ, затем получите графики V(1) и (V)2. Убедитесь, что V(1) — точная копия входного напряжения V ВХ. Выходное напряжение должно показать компоненту постоянного тока и сложную волну с максимумом в 3 В. Из теоретического изучения рядов Фурье можно заключить, что этот график напоминает периодическую волну, состоящую из основной и второй гармоник. Целесообразно распечатать копию этого графика для будущего изучения. На рис. 7.2 показаны эти графики.

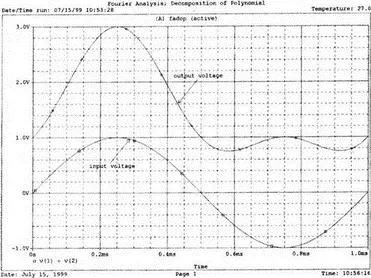
Рис. 7.2. Графики напряжений v 1и v 2для схемы на рис. 7.1

Рассмотрим также выходной файл для этой схемы (рис. 7.3), на котором показаны следующие значения для напряжений узлов: V(1)=0 В и V(2)=1 В. Это означает, что хотя входной сигнал не имеет смещения, выходное напряжение имеет смещение V(2)=1 В.

На рис. 7.3 в таблице компонентов ряда Фурье для V(1) не все компоненты имеют реальные значения. Так, значение постоянной составляющей теоретически должно быть равно нулю, но анализ дает очень малое значение 3.5Е-10, не равное в точности нулю из-за накопления ошибки округления.