Дж. Кеоун - OrCAD PSpice. Анализ электрических цепей

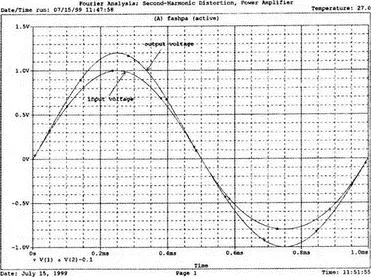
Рис. 7.6. Основная и вторая гармоники и результат их сложения

Выйдя из программы Probe, рассмотрите выходной файл для этого случая. Входное напряжение V(1) точно такое же, как и в предыдущем примере, но V(2), конечно, отличается. Обратите внимание, что постоянная составляющая выходного напряжения равна 0.2 В, а вторая гармоника при f =2 кГц имеет амплитуду 0,1 В и фазовый угол -90°. Другие гармоники намного меньше и ими можно пренебречь. В заключение определите общее гармоническое искажение, которое очень близко к 10%, как и ожидалось. Искажение по второй гармонике определено как b 1/ b 2где b 1и b 2— коэффициенты при второй и основной гармониках соответственно. Эти данные приведены на рис. 7.7.

Fourier Analysis; Second-Harmonic Distortion, Power Amplifier

Vin 1 0 sin(0 1 1000)

Rin 1 0 1MEG

E 2 0 poly(1) 1.0 0.1 1 0.2

Rout 2 0 1MEG

.TRAN 1us 1ms

.FOUR 1000 V(1) V(2)

.PROBE

.END

NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE

( 1) 0.0000 ( 2) .1000

FOURIER COMPONENTS OF TRANSIENT RESPONSE V(1)

DC COMPONENT = 2.936647E-08

HARMONIC FREQUENCY FOURIER NORMALIZED PHASE NORMALIZED

NO (HZ) COMPONENT COMPONENT (DEG) PHASE (DEG)

1 1.000E+03 1.000E+00 1.000E+00 1.115E-06 0.000E+00

2 2.000E+03 1.994E-08 1.994Е-08 -9.308E+01 -9.308E+01

3 3.000E+03 7.381E-09 7.381E-09 -9.083E+01 -9.083E+01

4 4.000E+03 4.388E-09 4.388E-09 -8.993E+01 -8.993E+01

5 5.000E+03 3.134E-09 3.134Е-09 -9.107Е+01 -9.107Е+01

6 6.000E+03 1.525E-09 1.525E-09 -6.706E+01 -6.706Е+01

7 7.000E+03 1.511E-09 1.511E-09 -1.392E+02 -1.392E+02

8 8.000E+03 1.237E-09 1.237E-09 -3.990E+01 -3.990E+01

9 9.000E+03 7.642E-10 7.642E-10 3.320E+01 3.320E+01

TOTAL HARMONIC DISTORTION = 2.208405E-06 PERCENT

FOURIER COMPONENTS OF TRANSIENT RESPONSE V(2)

DC COMPONENT = 2.000000E-01

HARMONIC FREQUENCY FOURIER NORMALIZED PHASE NORMALIZED

NO (HZ) COMPONENT COMPONENT (DEG) PHASE (DEG)

1 3.000E+03 1.000E+00 1.000E+00 7.683E-07 0.000E+00

2 2.000E+03 1.000E-01 1.000E-01 -9.000E+01 -9.000E+01

3 3.000E+03 1.756E-08 1.756E-08 -1.336E+02 -1.336E+02

4 4.000E+03 1.430E-08 1.430E-08 -1.348E+02 -1.348E+02

5 5.000E+03 9.547E-09 9.547E-09 -1.365E+02 -1.365E+02

6 6.000E+03 8.100E-09 8.100E-09 -1.232E+02 -1.232E+02

7 7.000E+03 6.463E-09 6.463E-09 -1.342E+02 -1.342E+02

8 8.000E+03 5.743E-09 5.743E-09 -9.544E+01 -9.544E+01

9 9.000E+03 6.931E-09 6.931E-09 -1.092E+02 -1.092E+02

TOTAL HARMONIC DISTORTION = 9.999880E+00 PERCENT

Рис. 7.7. Результаты анализа искажений по второй гармонике в усилителях

Используем простую схему (рис. 7.8), чтобы показать, как две синусоидальные волны объединяются в нелинейном устройстве, использующем довольно близкие друг к другу частоты, а именно f 1=1 кГц и f 2=1,5 кГц. Нелинейное смешивание происходит в зависимом источнике е-типа VCVS (ИНУН). Полином, описывающий связь, содержит больше членов, чем в предыдущем примере:

f ( x ) = 1 + x + х ² + x ³.

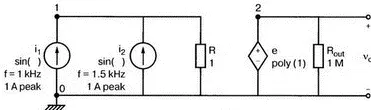
Рис. 7.8. Схема для демонстрации интермодуляционных искажений

Токи, суммируясь, создают в R= 1 Ом напряжение V(1), численно равное току в R. Таким образом, входное напряжение V(1) можно воспринимать как напряжение в нелинейном смесителе. Поскольку синусоидальные волны имеют различные частоты, их сумма представляет собой сложное периодическое колебание с частотой, отличной от частоты исходных составляющих (частотой биений). Входной файл:

Intermodulation Distortion

i1 0 1 sin(0 1 1000)

i2 0 1 sin(0 1 1500)

r 1 0 1

е20 poly(1) 1,0 1 1 1 1

rout 2 0 1MEG

.tran 50us 50ms 50us

.probe

.end

Проведите моделирование и получите в Probe V(1). Выберите Plot, X-Axis Settings…, User Defined, и установите диапазон от 0 до 10 мс, чтобы достичь установившегося входного напряжения. Этот график показан на рис. 7.9. Чтобы подтвердить, что он является фактически суммой гармонических составляющих с частотами 1 и 1,5 кГц, выберем Trace, Fourier, переходя из временной в частотную область. Изменим теперь границы по оси X , установив частотный диапазон от 4 до 12 кГц. Убедитесь, что параметры осей соответствуют нужным частотам и ожидаемым амплитудам. Фактически при f =1 кГц напряжение равно 0,991 В, а при f =1,5 кГц оно составляет 0,979 В. Не забывайте, что при этом синтезе присутствует некоторая ошибка накопления. На рис. 7.10 показана соответствующая амплитудно-частотная характеристика.

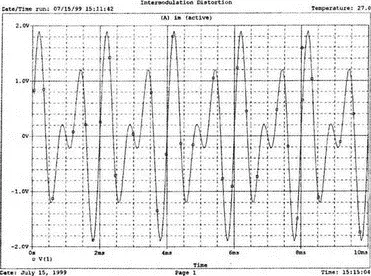
Рис. 7.9. Выходное напряжение при интермодуляционных искажениях

Рис. 7.10. Спектральный состав входного напряжения

Выберите затем Trace, End Fourier, чтобы возвратиться во временную область, удалите график V(1) и получите график напряжения на выходе смесителя V(2). Напомним, что смеситель представляет собой ИНУН с полиномиальной связью, заданной функцией f ( х ). Временная зависимость представляет собой график, подобный графику V(1), но при более внимательном рассмотрении можно обнаружить, что формы напряжений значительно отличаются. Кое-какие подсказки можно получить из гармонического состава этого сложного колебания, так что необходимо будет опять перейти в частотную область, выбрав диапазон по оси X от 0 до 5 кГц. Мы рекомендуем распечатать частотный спектр для дальнейшего изучения. Теоретический анализ компонентов частотной модуляции позволяет предсказывать и проверять результаты анализа на PSpice. Обратите внимание, что имеется постоянная составляющая в 2 В наряду со значительными составляющими в интервале от 0,5 до 4,5 кГц (смотри рис. 7.11 для частотного спектра).

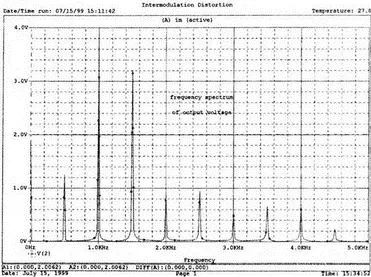
Рис. 7.11. Спектральный состав выходного напряжения

Простейшим для теоретического анализа является случай гармонического воздействия на цепь, состоящую из линейных компонентов, таких как резисторы, конденсаторы и катушки индуктивности, и, как вы знаете, при этом реакция представляет собой гармоническое колебание с той же частотой входного сигнала. Различные падения напряжения в схеме также представляют собой гармонические колебания с той же частотой, отличающиеся только по амплитуде и фазе. Используем простую схему, чтобы проиллюстрировать некоторые из этих свойств. На рис. 7.12 показаны три источника напряжения, питающие схему, содержащую резисторы R= 1 Ом и R 1 =R 2=0,001 Ом. Последние два резистора требуются, чтобы сделать источники напряжения неидеальными. Используя эту схему, мы можем показать сложение синусоидальных волн в Probe. Входной файл: