Дж. Кеоун - OrCAD PSpice. Анализ электрических цепей
- Название:OrCAD PSpice. Анализ электрических цепей
- Автор:
- Жанр:
- Издательство:ДМК Пресс, Питер
- Год:2008
- Город:Москва, Санкт-Петербург
- ISBN:978-5-9706-0009-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Дж. Кеоун - OrCAD PSpice. Анализ электрических цепей краткое содержание
Это руководство по работе в программе OrCAD Pspice предназначено для всех, кто знаком с основными разделами электротехники. При постепенном усложнении задач объясняются все необходимые аспекты работы в OrCAD Pspice, что позволяет творчески применять их при дальнейшем анализе электрических и электронных схем и устройств. Рассмотрение материала начинается с анализа цепей постоянного тока, продолжается анализом цепей переменного тока, затем переходит к различным разделам полупроводниковой электроники. Информация изложена таким образом, чтобы каждый, кто изучал или изучает определенный раздел электротехники, мог сразу же использовать OrCAD Pspice на практике. Больше внимания, чем в других книгах по этой теме, уделяется созданию собственных моделей и использованию встроенных моделей схем в OrCAD Pspice.
На прилагаемом к книге DVD вы найдете демонстрационную версию программы OrCAD PSpice Student Edition 9, которой можно пользоваться свободно. Кроме того, на диске размещена версия OrCAD 10.5 Demo Release, с которой можно работать в течение 30 дней после установки на компьютер.
OrCAD PSpice. Анализ электрических цепей - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
На рис. 8.1 все напряжения могут быть заменены токами, приводя к ситуации, дуальной по отношению к предыдущей. Это означает, что входным сигналом является ток i i , разностью — ток i d, выходным сигналом — ток i o=A id , а сигнал обратной связи становится равным v f =β i 0, обеспечивая равенство
i d=i i – i f .
Коэффициент усиления в петле обратной связи по-прежнему равен А β или, с учетом инверсии фазы, – А β. Коэффициент усиления при замкнутой цепи обратной связи, как и раньше, равен
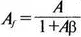
Генератор на базе моста Вина с начальным запуском
В качестве первого примера исследования генераторов рассмотрим генератор на базе моста Вина (рис. 8.2). Частота колебаний в схеме вычисляется из выражения:
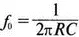
где R=R 1 =R 2и С = С 1= С 2. Примем ее равной f 0=25 кГц. Если выбрать значение С равным 1 нФ, то R= 6366 Ом. Для возникновения непрерывных колебаний отношение R f|R g должно быть равно 2. Если выбрать R f= 20 кОм, то R g =10 кОм. Попробуем использовать PSpice, чтобы показать, что колебания произойдут при необходимой частоте. Входной файл для такого анализа:
Wien-Bridge Oscillator
Е 2 0 4 1 2Е5
Ri 4 1 1Е6
Rg 1 0 10k
R1 3 4 6366
R2 4 0 6366
Rf 2 1 20k
C1 2 3 1nF IC=2V; начальный заряд для обеспечения колебаний
С2 4 0 1nF
.PROBE
.TRAN 0.05us 50us UIC
.END
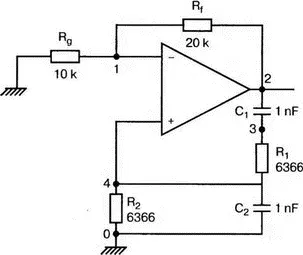
Рис. 8.2. Схема генератора на базе моста Вина
Конденсатору C 1сообщен начальный заряд (с помощью определенного начального напряжения), чтобы создать условия, требуемые для инициирования колебаний. Если не сделать этого, анализ на PSpice покажет выходное напряжение с устойчивым нулевым значением.
Результаты, полученные в Probe, показаны на рис. 8.3. График показывает выходное напряжение v(2). Обратите внимание, что оно представляет собой гармоническое колебание с частотой f =25 кГц и амплитудой в 6 В.
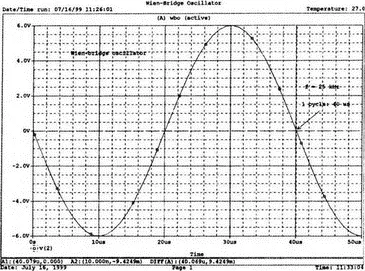
Рис. 8.3. Выходное напряжение генератора на базе моста Вина
Можно ли ожидать, что и реальный генератор даст амплитуду выходного напряжения в 6 В? Попытайтесь ответить на этот вопрос, выполнив анализ снова при начальном напряжении на конденсаторе IС=1V. Позже в этой главе мы рассмотрим также влияние на работу генератора коэффициента усиления петли обратной связи и фазового сдвига.
LC -генератор с начальным запуском
Генератор подстройки, использующий в цепи обратной связи два конденсатора и одну катушку индуктивности, назван генератором Колпитца. По схожей схеме построен и генератор Хартли, но в нем используются две катушки индуктивности и один конденсатор. Схема Колпитца и параметры ее компонентов показаны на рис. 8.4. Входной файл:
Colpitts Oscillator
Е 3 0 0 2 2Е5
Ri 0 2 1Е6
R1 2 1 10k
R2 2 3 20k
R 3 4 1k
C1 1 0 0.005uF
C2 4 0 0.05uF IC=2V
L 1 4 5mH
.PROBE
.TRAN 0.3us 60us UIC
.END
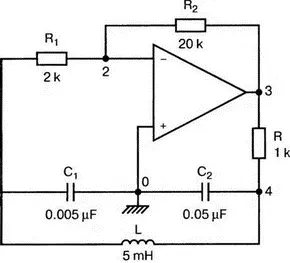
Рис. 8.4. Генератор Колпитца
Получите в Probe график выходного напряжения v(3), который показан на рис. 8.5. Убедитесь, что амплитуда возникших колебаний нарастает. Так как мы используем идеальный ОУ, в схеме не проявляется нелинейность. В практической схеме проявилось бы некоторое искажение синусоидальности колебания наряду со стабилизацией амплитуды.
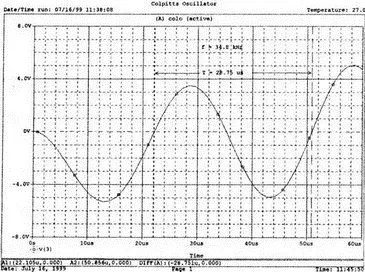
Рис. 8.5. Колебания в генераторе Колпитца
Амплитуда реального колебания определялась бы в значительной степени напряжением смещения ОУ. Обратите внимание, что частота определяется как величина, обратная периоду (разности между двумя моментами времени, в которых график напряжения пересекает ось X в одном направлении).
Измерения с помощью измерительной схемы
На рис. 8.6 представлена схема для измерения коэффициента усиления и фазового сдвига цепи обратной связи. Схема содержит независимый источник переменного напряжения V= 1 В, включенный между узлами TV 0и TV i (выходной и входной узел соответственно). Имеются также два ИНУН: EV i и EV 0. Независимый источник напряжения включается в подходящее место разрыва цепи обратной связи генератора. Каждый источник зависимого напряжения нагружен на сопротивление, чтобы узлы V i и V 0не оказались узлами с плавающим потенциалом. Измерительная методика будет проиллюстрирована в последующих примерах.
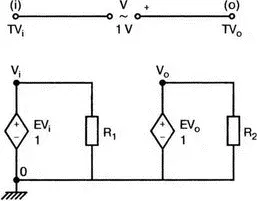
Рис. 8.6. Измерительная цепь для усилителей
Генератор со смещением фазы
Классический RC-генератор со смещением фазы показан на рис. 8.7. Выход ОУ связан с тремя фазосмещающими RC-цепочками. Каждая цепочка производит некоторый фазовый сдвиг, и если общий сдвиг фазы, произведенный в трех цепях, равен 180°, могут происходить колебания. Кроме того, требуется выполнение условия | A β|=1. Анализ схемы показывает, что частота колебаний
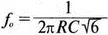
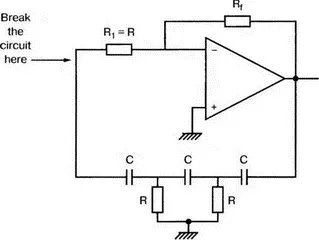
Рис. 8.7. Генератор со сдвигом фаз
Пусть, например, необходимо получить частоту колебаний f 0=100 Гц при С =0,5 мкФ и R =1,3 кОм. Анализ схемы также показывает, что при этом β=1/29; следовательно, чтобы возникли устойчивые колебания, величина | A | должна равняться 29. Практически величина | А | должна быть немного больше 29, чтобы компенсировать небольшие различия в параметрах компонентов и эксплуатационных режимах.
В схемах с инвертирующим ОУ величинам вычисляется из выражения:
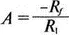
Поскольку R 1= R , это отношение преобразуется в
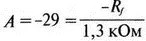
и, решая его относительно R f , мы найдем, что R f =37,7 кОм. Увеличив это значение на 5%, чтобы учесть ранее упомянутые отклонения, получим R f= 39,58 кОм.
Читать дальшеИнтервал:
Закладка:










