Дж. Кеоун - OrCAD PSpice. Анализ электрических цепей

Addition of Sine Waves of the Same Frequency

V1 1 0 sin (0 1 1kHz)

*Порядок следования параметров в сложном выражении для гармонических

*составляющих: смещение, амплитуда, частота, задержка, затухание, фаза

v2 2 0 sin(0 1 1kHz 0 0 45); фаза=45 градусов

v3 3 0 sin(0 1 1kHz 0 0 90); фаза=90 градусов

r1 1 2 0.001

r2 2 3 0.001

R 3 0 1

.tran 2us 2ms

.probe

.end

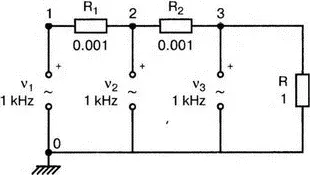
Рис. 7.12. Схема для сложения гармонических сигналов одной частоты

Выполните моделирование и в Probe получите графики v(1), v(2), и v=v(1)+v(2). Возникающие в результате графики показывают напряжение v 2с максимумом, отстающим приблизительно на 45° от максимума v 1, и суммарное напряжение v 1+ v 2с максимумом, расположенным между их максимальными значениями. Убедитесь, что максимум v 1=1 В достигается в момент 251 мкс (90°), максимум v 2=1 В — в момент 131 мкс (47,16°) и максимум v 1+ v 2=1,8381 В — в момент 171 мкс (61,56°). Удалите эти графики и получите временные зависимости для других комбинаций напряжений, например, для v(1), v(3) и v(1)+v(3). Основываясь на вашем умении складывать векторы напряжений, попытайтесь предсказать значение амплитуды для суммы напряжений до того, как получите графики в Probe, показанные на рис. 7.13.

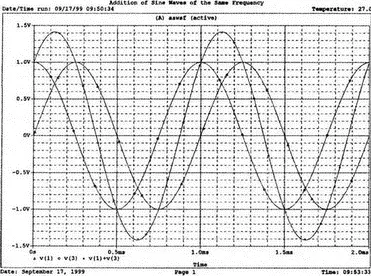
Рис. 7.13. Результат сложения гармонических сигналов одной частоты

Во входном файле, соответствующем схеме на рис. 7.12, можно легко варьировать параметры и состав источников питания. Удалим v 3и удвоим частоту напряжения v 2, чтобы она стала частотой второй гармоники для v 1. Конечно, результирующее колебание сразу станет несинусоидальным. Фактически форма его будет зависеть от соотношения фазовых углов v 1и v 2. Пусть в рассматриваемом примере обе гармоники достигают максимума одновременно. Входной файл для такого случая:

Adding Sine Waves; Fundamental and 2nd Harmonic Peaking Together

v1 1 0 sin(0 1 1kHz)

v2 2 0 sin(0 1 2kHz 0 0 -90)

R1 1 2 0.001

R 2 0 1

.tran 1us 1ms

.probe

.end

Проведите моделирование и получите в Probe графики v(1), v(2), и v=v(1)+v(2). Поскольку v 1и v 2достигают максимума одновременно, максимум результирующего колебания равен 2 В, но когда основная гармоника достигает отрицательного максимума, вторая гармоника возвращается к положительному максимуму, и их сумма обращается в нуль. Ясно, что суммарное колебание ( v 1+ v 2) несинусоидально. Эти графики приведены на рис. 7.14.

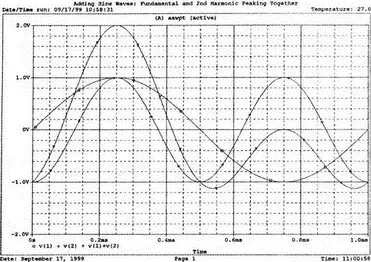
Рис. 7.14. Результат сложения первой и второй гармоник

Интересный график колебания, модулируемого по амплитуде, может быть получен в PSpice при использовании функции перемножения гармонических колебаний с существенно различными частотами. На рис. 7.15 показана схема, моделирующая такое устройство. Первым гармоническим источником является v 1с частотой 1 кГц. Второй источник v 2имеет частоту 20 кГц. Перемножение осуществляется в зависимом источнике е, представляющем собой ИНУН (VCVS). Резисторы необходимы, чтобы избежать появления плавающих потенциалов. Входной файл:

Multiplier for Modulated Wave

v1 1 0 sin(0 1 1000)

R1 1 0 10k

v2 2 0 sin(0 1 20000)

R2 2 0 10k

e 3 0 poly (2) 1,0 2,0 0 0 0 0 1

R3 2 0 10k

.tran 1us 1ms

.four 1000 v(1) v(2) v(3)

.probe

.end

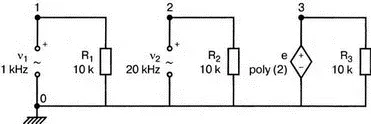
Рис. 7.15. Умножитель для модуляции синусоидального колебания

Пять последних записей в команде ввода полиномиального источника: 0 0 0 0 1. Вспомним, что это — значения коэффициентов в членах k 0, k 1 v 1, k 2 v 2, k 3 v 12и k 4 v 1 v 2. Все значения равны 0 за исключением k 4, который равен 1.

Проведите моделирование и получите в Probe графики v(1) и v(3). На общем графике намеренно не построена гармоническая составляющая с частотой 20 кГц, чтобы не усложнять понимание процессов. Результирующее колебание v(3) имеет классический вид амплитудно-модулированного колебания. В этом примере обе входные гармоники v 1и v 2имеют амплитуду 1 В. Графики приведены на рис. 7.16.

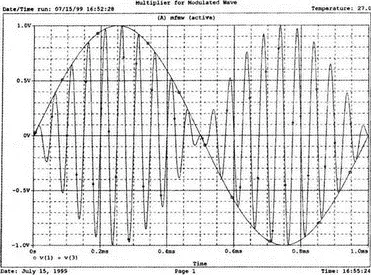
Рис. 7.16. Результат исследования амплитудно-модулированных сигналов

Не выходя из Probe, добавьте график другого входного напряжения v(2) так, чтобы отобразить все напряжения: v(1), v(2) и v(3). Теперь этот график содержит, наряду с двумя другими волнами, и несущую, давая законченное изображение. Получите распечатку для дальнейшего изучения, затем удалите график v(2) и выберите Trace, Fourier. Установите по оси X границы диапазона от 0 до 30 кГц. В частотной области теперь отображаются составляющие с частотами 1,19 и 21 кГц. Последние компоненты представляют собой верхнюю и нижнюю побочные частоты, возникшие при такой модуляции. Определите амплитуду каждой из этих волн. Вспомните тригонометрическое тождество,

(sin a )(sin b ) = 0.5[cos( a – b ) – cos( a + b )],

которое объясняет амплитуды 0,5 В для частот боковой полосы. Обратитесь к рис. 7.17, на котором изображен частотный спектр. (Маркеры были удалены для получения более ясной картинки.) Проведите анализ с различными относительными амплитудами для напряжения модуляции v 1, чтобы видеть, какое влияние это оказывает на глубину модуляции т . Например, когда v 1имеет амплитуду 0,8, что является глубиной модуляции и что напоминает результирующее колебание?

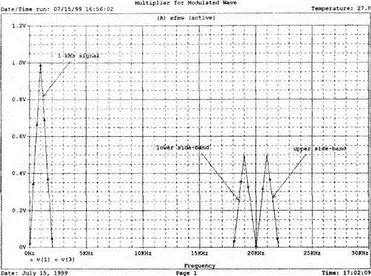
Рис. 7.17. Частотный спектр амплитудно-модулированного колебания

.FOUR <���частота>*<���выходные переменные>

Например, запись

.FOUR 1kHz V(1) V(2)

показывает, что выполняется разложение в ряд Фурье. Разложение может быть выполнено только после получения временной зависимости для установившегося режима, полученной при анализе переходного процесса. Такая команда должна присутствовать во входном файле:

.TRAN <���шаг><���момент окончания>