Дж. Кеоун - OrCAD PSpice. Анализ электрических цепей

Fourier Analysis; Decomposition of Polynomial

Vin 1 0 sin(0 1 1000); arguments are offset, peak, and frequency

Rin 1 0 1MEG

E 2 0 poly(1) 1,0 1 1 1; last 3 1s are for k0, k1, k2

Rout 2 0 1MEG

.TRAN 1us 1ms

.FOUR 1000 V(1) V(2)

.PROBE

.END

NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE

( 1) 0.0000 ( 2) 1.0000

FOURIER COMPONENTS OF TRANSIENT RESPONSE V(1)

DC COMPONENT = 2.936647E-08

HARMONIC FREQUENCY FOURIER NORMALIZED PHASE NORMALIZED

NO (HZ) COMPONENT COMPONENT (DEG) PHASE (DEG)

1 1.000E+03 1.000E+00 1.000E+00 1.115E-06 0.000E+00

2 2.000E+03 1.994E-08 1.994E-08 -9.308E+01 -9.308E+01

3 3.000E+03 7.381E-09 7.381E-09 -9.083E+01 -9.083E+01

4 4.000E+03 4.388E-09 4.388E-09 -8.993E+01 -8.993E+01

5 5.000Е+03 3.134Е-09 3.134Е-09 -9.107Е+01 -9.107Е+01

6 6.000E+03 1.525E-09 1.525E-09 -6.706E+01 -6.706E+01

7 7.000E+03 1.511E-09 1.511E-09 -1.392E+02 -1.392E+02

8 8.000E+03 1.237E-09 1.237E-09 -3.990E+01 -3.990E+01

9 9.000E+03 7.642E-10 7.642E-10 3.320E+01 3.320E+01

TOTAL HARMONIC DISTORTION = 2.208405E-06 PERCENT

FOURIER COMPONENTS OF TRANSIENT RESPONSE V(2)

DC COMPONENT = 1.500000E+00

HARMONIC FREQUENCY FOURIER NORMALIZED PHASE NORMALIZED

NO (HZ) COMPONENT COMPONENT (DEG) PHASE (DEG)

1 1.000E+03 1.000E+00 1.000E+00 -2.888E-07 0.000E+00

2 2.000E+03 5.000E-01 5.000Е-01 -9.000E+01 -9.000E+01

3 3.000E+03 7.971E-08 7.971E-08 -1.546E+02 -1.546E+02

4 4.000E+03 5.126Е-08 5.126Е-08 -1.439E+02 -1.439E+02

5 5.000E+03 3.918E-08 3.918E-08 -1.420E+02 -1.420E+02

6 6.000E+03 3.327E-08 3.327E-08 -1.299E+02 -1.299E+02

7 7.000Е+03 3.606E-08 3.606E-08 -1.268Е+02 -1.268E+02

8 8.000E+03 2.889E-08 2.859E-08 -1.316E+02 -1.316E+02

9 9.000E+03 2.584E-08 2.584E-08 -1.189Е+02 -1.189Е+02

TOTAL HARMONIC DISTORTION = 4.999939E+01 PERCENT

Рис. 7.3. Выходной файл с результатами анализа схемы на рис. 7.1

Первая гармоника представляет собой основную гармонику при f =1 кГц. Показана амплитуда первой гармоники ряда Фурье и ее фаза 2.4Е-7 (тоже почти ноль). Если считать, что этот компонент выражен формулой

b n sin( nx ),

то это означает, что b 1=1, n =1, где индекс 1 соответствует основной частоте. Другие гармоники могут игнорироваться, так как их амплитуды на много порядков меньше основной гармоники. Именно основная гармоника отражена на графике V(1) в Probe, получена она из данных на рис. 7.3.

Другая таблица компонентов Фурье на рис. 7.3 относится к V(2). При просмотре различных гармоник обратите внимание, что имеется постоянная составляющая в 1,5 В. Почему 1,5 В? Составляющая k 0=1 В дает только часть этого значения, остальные же 0,5 В связаны со второй гармоникой. Теория показывает, что при гармоническом искажении по второй гармонике в выходном напряжении кроме собственно второй гармоники с амплитудой b 2появляется и связанная с искажениями по второй гармонике постоянная составляющая со значением b 0= b 2. Амплитуда основной частоты в разложении равна b 1=1 В, амплитуда второй гармоники b 2=0,5 В, ее фазовый угол составляет -90°. Более высокие гармоники имеют намного меньшую величину и их можно не учитывать.

В качестве упражнения по гармоническому синтезу вы можете нарисовать отдельные гармоники и сложить их, чтобы предсказать результат, который вы получите в Probe для V(2). Не забудьте учесть постоянную составляющую и соответствующие амплитуды и фазы для основной и второй гармоник. После того как вы нарисуете результирующее колебание, вам, несомненно, будет приятно узнать, что PSpice может сделать эту нудную работу за вас.

Создадим новый входной файл, соответствующий рис. 7.4, на котором к схеме рис. 7.1 добавлены еще два независимых источника тока.

Мы использовали два источника только для того, чтобы вы могли получить основную и вторую гармоники на одном графике с выходным напряжением. Дополнительные источники питают подключенный параллельно 1-омный резистор. Такое изменение первоначальной схемы совсем не обязательно, просто оно оказалось удобным при данном наборе параметров. Новый входной файл представляет собой расширение предыдущего файла и выглядит следующим образом:

Fourier Analysis; Decomposition of Polynomial

Vin 1 0 sin(0 1 1000);аргументы - смещение, амплитуда и частота

Rin 1 0 1MEG

Е 2 0 poly(1) 1,0 1 1 1; последние 3 записи for k0, k1, k2

Rout 2 0 1MEG

i1 0 3 sin(1 1 1000)

i2 0 3 sin(0.5 0.5 2000 0 0 -90)

r 3 0 1

.TRAN 1us 1ms

.FOUR 1000 V(1) V(2) V(3)

.PROBE

.END

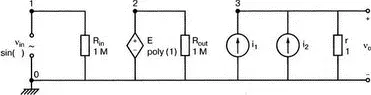
Рис. 7.4. Схема для анализа сложения гармоник и разложения в ряд Фурье

Перед выполнением анализа подробно рассмотрим описания для i 1и i 2. Для гармонического синтеза используются результаты разложения в ряд Фурье из предыдущей задачи. Убедитесь, что вы понимаете смысл всех параметров; затем выполните анализ в Probe, получив графики I(i1), I(i2) и I(r). Хотя они и представляют собой токи, но численно они равны напряжениям, так как проходят через сопротивление в 1 Ом. На рис. 7.5 представлены результаты. Теперь можно установить, что первый график представляет собой основную гармонику, второй — вторую гармонику, а третий — результат сложения их в резисторе r . Конечно, можно получить график V(3) вместо I(r). При этом ось Y будет размечена в единицах напряжения, а не тока. Убедитесь, что сумма двух первых кривых дает третью кривую в различные моменты времени. Чтобы сделать график более компактным, мы использовали смещение в 1 В для основной гармоники и в 0,5 В — для второй гармоники. Фактически основная гармоника имеет нулевое смещение.

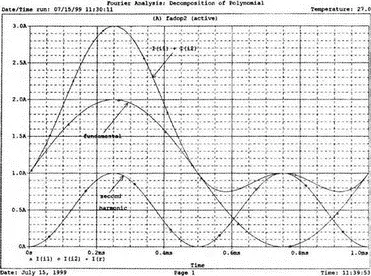
Рис. 7.5. Основная и вторая гармоники и результат их сложения

Когда рабочая область усилителя выходит за пределы линейной части характеристики, это приводит к некоторым искажениям. Первое приближение к реальной выходной кривой достигается включением в модель второй гармоники, показывающей, что переходная функция, связывающая i c и i b (ток коллектора и базы), является некоторой параболой. Обычно искажение намного меньше, чем принятое в нашем первом, вводном, примере, который был показан на рис. 7.1. Более точный полином задается формулой

f ( x ) = 0,1 + x + 0,2 x ².

Достаточно просто преобразовать первоначальный входной файл, чтобы он отражал эту ситуацию. Команда ввода для зависимого источника Е примет вид:

Е 2 0 poly(1) 1,0 0.1 1 0.2; последние три величины для k0, k1, k2

а весь входной файл будет:

Fourier Analysis; Second-Harmonic Distortion, Power Amplifier

Vin 1 0 sin(0 1 1000)

Rin 1 0 1MEG

E 2 0 poly(1) 1,0 0.1 1 0.2

Rout 2 0 1MEG

.TRAN 1us 1ms

.FOUR 1000 V(1) V(2)

.PROBE

.END

Проведите анализ и получите в Probe графики V(1) и V(2). Вы увидите, что обе волны выглядят, как настоящие синусоиды. Для более точного сравнения удалите график V(2) и получите вместо него график V(2)–0,1. Это позволит сблизить обе кривые. При сравнении волн не забудьте, что V(1) представляет собой просто синусоидальный сигнал, a V(2) — комбинацию основной и второй гармоник. В этом примере вторая гармоника значительно меньше по амплитуде, чем в предыдущем. Вы можете распечатать результаты исследования, приведенные на рис. 7.6.