Журнал Компьютерра - Журнал «Компьютерра» №27-28 от 26 июля 2005 года

Сами казино - в отличие от игроков - предпочитают не полагаться на удачу. За редким исключением (блэкджек, покер) игры, которые можно найти в казино, «спроектированы» так, что заведение в долгосрочной перспективе в накладе не останется. В общем случае обанкротить казино игроки могут, лишь если перестанут в него заходить.

Рулетка не является исключением. Игрок находится в менее выгодном положении. У него и казино почти равные шансы, но с помощью зеро и (в американском варианте колеса) двойного зеро казино обеспечивает себе перевес. За счет зеро вероятность выигрыша для игрока, ставящего на красное, составляет не 50%, как можно было бы ожидать, а 48,65% (18/37). Ровно такая же ситуация у игрока, ставящего на черное. Разница между суммой шансов двух игроков, чьи ставки покрывают почти всю поверхность стола, и суммой вообще всех шансов часто называется долей заведения. На рулетке с одним зеро доля заведения составляет 2,7% (1/37). На рулетке с двойным зеро она вдвое больше.

Чтобы привлечь игроков, владельцы казино порой вводят дополнительные правила, призванные уменьшить свою долю и повысить шансы игрока. Одно из самых распространенных дополнений заключается в том, что фишки, проигранные заведению на зеро, сгорают не сразу. Вместо этого игроку предоставляется выбор: либо он забирает половину своей ставки сразу, либо оставляет ставку на следующий круг. Если она выиграет, игроку отдают ставку целиком (но без выигрыша). Это правило уменьшает долю заведения примерно вдвое.

Математика рулетки очень проста. «Шарик не имеет памяти», каждая ставка абсолютно независима, вероятность выигрыша любой человек может представить в уме (хотя бы в виде натуральной дроби). И тем не менее неглупые, казалось бы, люди тратят годы на разработку оптимальных стратегий, призванных сделать игру в рулетку прибыльной.

Дело в том, что поверить в убыточность рулетки мешает элементарный здравый смысл. Да, разумеется, мы не можем повлиять на колесо, но ведь есть еще один параметр - размер ставок. Не нужно быть семи пядей во лбу, чтобы придумать стратегию, которая в конечном счете гарантирует игроку выигрыш. Для достижения такого результата нужно всего лишь каждый раз увеличивать ставку в несколько раз. Рано или поздно удача повернется к игроку лицом, и он не только вернет свои деньги, но еще и обыграет казино.

Стратегия, основанная на удвоении ставки при каждом проигрыше, называется Мартингейл и является, наверное, самой старой системой игры в рулетку. В идеальном случае она действительно гарантирует выигрыш, однако для этого требуется выполнение сразу нескольких условий:

у игрока, пользующегося системой Мартингейл, должен быть бездонный карман;

в казино не должно быть ограничения на максимальный размер ставки.

Очевидно, что второе условие сильнее первого. Если в казино установлен максимальный размер ставки (а в современных заведениях так и сделано, без исключений), то финансовая состоятельность игрока для исхода игры значения не имеет. Кроме того, эффективность применения Мартингейла даже при удачном стечении обстоятельств вызывает большие сомнения (см. табл. 1):

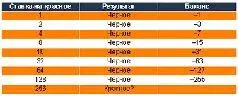
Выиграв на девятом шаге, мы можем заработать 256 долларов, что всего на доллар больше, чем мы уже потратили. Проигрыш увеличит сумму наших затрат до 511 долларов. Шансы при этом не меняются и составляют 18/37. По сути, благодаря следованию системе Мартингейл мы вынуждены поставить 256 долларов, чтобы выиграть всего один доллар. И сколько бы мы ни играли, максимум, что может обеспечить Мартингейл, - выигрыш в размере первоначальной ставки.

Опыт подсказывает нам, что шарик, девять раз подряд попадающий на черное, - событие крайне маловероятное (18/37 в девятой степени, или 0,1526%). К сожалению, низкая вероятность этого события не имеет никакого отношения к тому, что сейчас шарик с одинаковой вероятностью может попасть как на красное, так и на черное, и с меньшей, но ненулевой вероятностью - упадет на зеро. Вероятность попадания шарика на любой из цветов ничуть не отличается от обычной и равна 18/37.

Это, в свою очередь, не исключает того, что бесконечные или просто длинные серии постоянно удваиваемых ставок опасны для казино. Поэтому в большинстве игорных заведений правила составлены таким образом, что при удвоении вы до девятого шага просто не доберетесь - максимальная разрешенная ставка в лучшем случае будет в сто раз выше минимальной, что дает нам не более семи шагов, а как правило - не более пяти.

Вернемся на минутку к шарику, девять раз подряд падающему на черное. Если рассматривать серию ставок в совокупности, то шансов на то, что неблагоприятная для игрока серия прервется сыгравшей ставкой, действительно больше (необязательно, конечно, на девятом шаге). Другими словами, игроки, работающие по системе Мартингейл, на самом деле чаще выигрывают. Однако это нисколько не улучшает их благосостояния, потому что частые мелкие выигрыши с лихвой компенсируются нечастыми, но очень крупными проигрышами.

Система, правилами которой предписывается увеличивать ставку на проигрыше, называется системой с негативной прогрессией. Кроме классического Мартингейла системами с негативной прогрессией являются Супер-Мартингейл (здесь игрок удваивает ставку и добавляет к ней еще один номинал, то есть прогрессия выглядит следующим образом: 1-3-7-15-31…), Голландская Система (1-3-5-7-9; в этом случае для покрытия убытков одного выигрыша будет недостаточно) и т. д.

К системам с негативной прогрессией можно отнести и систему д’Аламбера[В статьях Д. Лесного, опубликованных на www.cgm.ru, термин «система д’Аламбера» используется для обозначения всех систем с негативной прогрессией, а описываемая система называется «системой Томаса Дональда»], по которой игрок должен увеличивать ставку на единицу при проигрыше и уменьшать на единицу при выигрыше. Игра ведется только на равные шансы (то есть игрок ставит либо на красное-черное, либо на чет-нечет). Система построена на предположении, что в серии спинов красное и черное выпадают относительно равномерно. На практике это не так: почти одноцветные серии не такая уж и редкость. В оправдание д’Аламбера следует сказать, что сам он в подобные системы не верил, и его именем система названа скорее по недоразумению.

Еще одна популярная система - Cancellation - довольно сложна в применении, но по сути не слишком отличается от Мартингейла (табл. 2). Перед тем как сделать первую ставку, игрок на бумажке выписывает десять чисел. Первая ставка - это сумма первого и последнего числа (в нашем случае - 11 фишек). Если ставка сыграла, то «счастливые номера» зачеркиваются, последовательность на два числа уменьшается, а мы переходим к следующей граничной паре чисел. Если ставка проиграла, то нижнее число увеличивается на сумму этих двух чисел (в нашем случае - 11 фишек на первом проигрыше, но на самом деле числа могут быть любыми; с тем же успехом начальная последовательность могла состоять из десяти единиц, тогда мы бы увеличивали «несчастливый номер» при первом проигрыше на два). И так, пока не окажутся зачеркнутыми все числа.